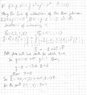- #1
jegues
- 1,097
- 3
Homework Statement
See first figure.
Homework Equations
N/A
The Attempt at a Solution
See second figure. I defined direction of the line by which the two planes intersect as,
[tex]\vec{d}[/tex]
and found that the point they are asking about is when,
[tex]t=1[/tex]
and I'm stuck here. This is my first attempt at a question like this so I applogize in advance if I'm missing something obvious.
How do I figure out what direction is the direction of increasing x?
[tex]D_{u^{+}}f(x,y,z) = f_{x}(x,y,z)a + f_{y}(x,y,z)b + f_{z}(x,y,z)c[/tex]
So,
[tex]D_{u^{+}}f(x,y,z) = ax^{2} + b2y -c2z [/tex]
At the point (-1,1,3),
[tex]D_{u^{+}}f(-1,1,3) = a + 2b -6c[/tex]
This is as far as I got.
Any suggestions?