- #1
Karol
- 1,380
- 22
Homework Statement
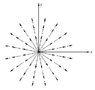
The question is to draw the function:
[tex]V=\frac {\boldsymbol{\hat {r}}}{r^2}[/tex]
And to compute it's divergence: [itex]\nabla \cdot V[/itex]
Homework Equations
[tex]\nabla\cdot V=\left ( \frac {\partial}{\partial x} \boldsymbol{\hat {x}}+\frac {\partial}{\partial y} \boldsymbol{\hat {y}}+\frac {\partial}{\partial z} \boldsymbol{\hat {z}}\right )\left ( v_x \boldsymbol{\hat {x}}+v_y \boldsymbol{\hat {y}}+v_z \boldsymbol{\hat {z}}\right )=\frac {\partial v_x}{\partial x}+\frac {\partial v_y}{\partial y}+\frac {\partial v_z}{\partial z}[/tex]
The Attempt at a Solution
[tex]V=\frac {x}{x^2+y^2+z^2}\boldsymbol{\hat {x}}+\frac {y}{x^2+y^2+z^2}\boldsymbol{\hat {y}}+\frac {x}{x^2+y^2+z^2}\boldsymbol{\hat {x}}[/tex]
The x component:
[tex]\frac {\partial}{\partial x}\left( \frac {x}{x^2+y^2+z^2}\right)=\frac {-2x^2+y^2+z^2}{(x^2+y^2+z^2)^2}[/tex]
And the other components are similar
I don't think this is the answer, since i was told to expect something special, maybe a number?
The vector field is, to my opinion, as in the picture attached