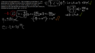Dividing 480/(-1.6x10^(-19))

[HazyMan]

1. A capacitor with a capacity of C= 20μF is connected to a source with a voltage of V=24V. We unplug the source from the capacitor and we then connect it with a wire and the capacitor gets charged in a time of Δt=0.2s. Figure out the number of electrons that pass go to the capacitor and the current. Given: -1.6x10^-19

2. q=C⋅V , x=q/e , I=q/t

3. A picture should be somewhere in the forum, showing a solution attempt. By the way, i am only stuck at question 2). I only need to learn how to divide such kind of numbers and then the exercise will be complete.

 

[fresh_42]

The trick is to write the quotient in terms you can handle: What does $\mu$ mean? Where are the Coulombs in the denominator have gone to? Can you write $1.6 \cdot 10^{-19}$ as $16 \cdot\ldots \,$? How would you handle $\dfrac{a\cdot b}{c \cdot d}$ if $c\,|\,a$ and $d\,|\, b\,?$

 

[HazyMan]

The trick is to write the quotient in terms you can handle: What does $\mu$ mean? Where are the Coulombs in the denominator have gone to? Can you write $1.6 \cdot 10^{-19}$ as $16 \cdot\ldots \,$? How would you handle $\dfrac{a\cdot b}{c \cdot d}$ if $c\,|\,a$ and $d\,|\, b\,?$

Are you trying to give examples or are you actually asking? If you're asking, μC means microcoulomb and i forgot to add the symbol in the denominator, sorry.

 

[fresh_42]

Are you trying to give examples or are you actually asking? If you're asking, μC means microcoulomb and i forgot to add the symbol in the denominator, sorry.

I actually ask, because the answers to those questions will guide you to the solution. Btw., I wanted to know the numerical value of micro, not it's writing.

 

[HazyMan]

I actually ask, because the answers to those questions will guide you to the solution. Btw., I wanted to know the numerical value of micro, not it's writing.

Ok, so:
1C is equal to 1.000.000μC.
Is that what you mean? I'm sorry for any irrelevant answers i might reply with.

 

[fresh_42]

Ok, so:
1C is equal to 1.000.000μC.
Is that what you mean? I'm sorry for any irrelevant answers i might reply with.

Yes, but it is the complicated answer, as you said $1= 1,000,000\mu$ which means $\mu = \frac{1}{1,000,000}$. No write this in powers of $10$, and also solve $1.6\cdot 10^{-19}=16 \cdot 10^{z}$. What is $z$?

 

[HazyMan]

Yes, but it is the complicated answer, as you said $1= 1,000,000\mu$ which means $\mu = \frac{1}{1,000,000}$. No write this in powers of $10$, and also solve $1.6\cdot 10^{-19}=16 \cdot 10^{z}$. What is $z$?

What do you mean with powers of 10? Also, what does z mean?

 

[fresh_42]

What do you mean with powers of 10? Also, what does z mean?

Do you know what $10^{-1}$ stands for? If yes, then what is $\mu = \dfrac{1}{1,000,000}\,?$
Before you solve a problem, you should understand it, especially what your symbols mean.
$z$ is the power, which makes $1.6 \cdot 10^{-19}$ into $16 \cdot \ldots$

 

[Ray Vickson]

What do you mean with powers of 10? Also, what does z mean?

Google "powers of 10" to see numerous explanatory articles, with examples. It is not difficult, but it may be unfamiliar to you; if so, you need to remedy that, especially if you plan to study physics or engineering.

 

[HazyMan]

Do you know what $10^{-1}$ stands for? If yes, then what is $\mu = \dfrac{1}{1,000,000}\,?$
Before you solve a problem, you should understand it, especially what your symbols mean.
$z$ is the power, which makes $1.6 \cdot 10^{-19}$ into $16 \cdot \ldots$

ok so I'm replying late, but: μ= 1/10⁶.
now what is left is finding what the Z is
EDIT: I figured out the Z to be -20.
1.6x10^-19=16x10^-20

 

[HazyMan]

Today i came up with this. Is it correct?

 

[fresh_42]

Today i came up with this. Is it correct?

The $3$ is correct, but you have to collect the right number of digits, will say powers of $10$. And, yes, $1.6\cdot 10^{-19}=16\cdot 10^{-20}$. So we have $-x=\dfrac{480\,\mu C}{1.6\cdot 10^{-19}C}= \dfrac{480\,\mu C}{16\cdot 10^{-20}C}= \dfrac{480}{16}\cdot \dfrac{\mu}{10^{-20}}\cdot \dfrac{C}{C}\,.$

Now where has the $\mu$ gone to? And what is the power $n$ in $\dfrac{480}{16}= 3\cdot 10^n\,?$

Although your notations are a bit confusing, I think you have everything write ($n=1\; , \;\dfrac{1}{10^{-20}}=10^{20}$), except that you seem to have forgotten the micro!

 

[HazyMan]

The $3$ is correct, but you have to collect the right number of digits, will say powers of $10$. And, yes, $1.6\cdot 10^{-19}=16\cdot 10^{-20}$. So we have $-x=\dfrac{480\,\mu C}{1.6\cdot 10^{-19}C}= \dfrac{480\,\mu C}{16\cdot 10^{-20}C}= \dfrac{480}{16}\cdot \dfrac{\mu}{10^{-20}}\cdot \dfrac{C}{C}\,.$

Now where has the $\mu$ gone to? And what is the power $n$ in $\dfrac{480}{16}= 3\cdot 10^n\,?$

Although your notations are a bit confusing, I think you have everything write ($n=1\; , \;\dfrac{1}{10^{-20}}=10^{20}$), except that you seem to have forgotten the micro!

All i did was 48/16 (i took out the 0 from 48) which gave me 3. then i added the 0 that i took, and put it in ^-20-, which gave me ^-21-. That's how i came up with 3x10²¹

 

[fresh_42]

All i did was 48/16 (i took out the 0 from 48) which gave me 3. then i added the 0 that i took, and put it in ^-20-, which gave me ^-21-. That's how i came up with 3x10²¹

Yep, that was right. However, the question remains: Where did the $\mu$ go to?

 

[HazyMan]

Yep, that was right. However, the question remains: Where did the $\mu$ go to?

Well I'm kinda confused. Did i have to add in 480/16 x 1000000/10^-20 where 480/16 x μ/10^-20?

 

[fresh_42]

Well I'm kinda confused. Did i have to add in 480/16 x 1000000/10^-20 where 480/16 x μ/10^-20?

Sure, only that $\mu \neq 1000000$ but $\mu = 0.000001 = 10^{-6}$. If you had to walk $10\,km$, would you equal this to $10\,m$? The $\mu$ (micro) is nothing else than the $k$ (kilo). Have a look: https://en.wikipedia.org/wiki/Unit_prefix All these prefixes only abbreviate a multiplicative factor of a power of ten! For a kilo we have a thousand (times), for a milli we have a thousandth (times), a giga is a billion (times), a nano a billionth (times) and so on.

 

[HazyMan]

Sure, only that $\mu \neq 1000000$ but $\mu = 0.000001 = 10^{-6}$. If you had to walk $10\,km$, would you equal this to $10\,m$? The $\mu$ (micro) is nothing else than the $k$ (kilo). Have a look: https://en.wikipedia.org/wiki/Unit_prefix All these prefixes only abbreviate a multiplicative factor of a power of ten! For a kilo we have a thousand (times), for a milli we have a thousandth (times), a giga is a billion (times), a nano a billionth (times) and so on.

yea sorry i got that wrong. what else is left now, for the exercise to be complete?

 

[fresh_42]

yea sorry i got that wrong. what else is left now, for the exercise to be complete?

I'm not quite sure what you need. What you have so far is $x=3\cdot 10^{21} \cdot \mu\,$ [no units anymore!] so you need to replace $\mu$ which yield the correct $x$ which I think is all that's left.

 

[HazyMan]

I'm not quite sure what you need. What you have so far is $x=3\cdot 10^{21} \cdot \mu\,$ [no units anymore!] so you need to replace $\mu$ which yield the correct $x$ which I think is all that's left.

well I've definitely gotten some help from this thread, however i am left quite confused. the 3x10²¹ are meant to be electrons that went into the exercise's capacitor as it got charged in 0.2 seconds. however the 0.2 seconds are not any helpful in the specific equation/division that I am trying to solve. anyway, thank's for your help, it's greatly appreciated!

 

[fresh_42]

well I've definitely gotten some help from this thread, however i am left quite confused. the 3x10²¹ are meant to be electrons that went into the exercise's capacitor as it got charged in 0.2 seconds. however the 0.2 seconds are not any helpful in the specific equation/division that I am trying to solve. anyway, thank's for your help, it's greatly appreciated!

$10^{21}\neq 10^{21}\mu = 10^n$. What is $n$?

I get: $I=2,4\, mA\; , \;Q=480 \,\mu C$ and $x$ electrons. I think you had $I=24\,mA$ which is too high.

 

[HazyMan]

$10^{21}\neq 10^{21}\mu = 10^n$. What is $n$?

how is 10²¹ not equal to 10²¹?

 

[fresh_42]

how is 10²¹ not equal to 10²¹?

That is not what I wrote. I said $1.000.000.000.000.000.000.000 \neq 1.000.000.000.000.000.000.000\cdot$μ
You must multiply by $\mu = 0,000001 = \dfrac{1}{1.000.000}$ same as a marathon isn't 42,195 meters, it is 42,195 kilometers, which is $42,195 \,km=42,195 \cdot k \cdot m= 42,195 \cdot 1000 \cdot m = 42.195 \,m$. That's a lot more than 42 meter, and $10^{21}\cdot \mu$ is a lot less than $10^{21}\,.$

 

[HazyMan]

$10^{21}\neq 10^{21}\mu = 10^n$. What is $n$?

I get: $I=2,4\, mA\; , \;Q=480 \,\mu C$ and $x$ electrons. I think you had $I=24\,mA$ which is too high.

24mA is actually the correct answer. my solutions book says so, it just doesn't exactly explain the procedure to finding it but that one is fine

 

[HazyMan]

$10^{21}\neq 10^{21}\mu = 10^n$. What is $n$?

I get: $I=2,4\, mA\; , \;Q=480 \,\mu C$ and $x$ electrons. I think you had $I=24\,mA$ which is too high.

is n 10¹⁵?

 

[HazyMan]

Okay soo, could you explain the entire procedure we went through to solve the exercise, in one text/reply? Maybe that would help me out more

 

[fresh_42]

24mA is actually the correct answer. my solutions book says so, it just doesn't exactly explain the procedure to finding it but that one is fine

Yes, you are right. I used $0,2\,s$ instead of $0,02\,s$.

 

[fresh_42]

O.k. but only as we already have all ingredients.

We have given: a capacity of $Cap=20 \,\mu F =20\,\mu \frac{C}{V}$, a voltage of $U= 24\,V$ and a time span of $t=0,02\,s\,.$

I will use the comma as separation sign, that is I will write $\frac{1}{2}=0,5\,.$ I think we are both used to this standard and I don't want to confuse you with a point as separator (American notation). I also write $Cap$ for capacity, to avoid confusion with the $C$ for Coulomb; and $U$ for voltage, to avoid confusion with $V$ for Volt. $F$ are Farad, and $As$ Ampère times seconds.

I first calculated the load, same as you did:
$$Q=Cap \cdot U=20 \cdot \frac{\mu C}{V}\cdot 24\,V=480\mu \cdot C= 480 \cdot 10^{-6} \cdot C = 480 \cdot 10^{-6}\, A\cdot s$$
This results in a current, same as you did:
$$
I=\dfrac{Q}{t}=\dfrac{480 \mu \,As}{0,02\,s}=\dfrac{48000 \cdot 10^{-6}\,As}{2\,s}= 24000\cdot 10^{-6} \,A = 24 \cdot 10^{3}\cdot 10^{-6}\,A=24 \cdot 10^{-3}
\,A= 24\,mA
$$
And last the number of electrons, which you denoted by $x$:
$$
x=\dfrac{Q}{e}=\dfrac{480\,\mu C}{1,6\cdot 10^{-19}\, C}=\dfrac{4800}{16} \cdot 10^{-6} \cdot \dfrac{1}{10^{-19}}=300 \cdot 10^{-6+19}=3 \cdot 10^2 \cdot 10^{13}= 3\cdot 10^{15}
$$

As an additional homework, I give you this to read: https://www.physicsforums.com/insights/10-math-tips-save-time-avoid-mistakes/

 

[HazyMan]

O.k. but only as we already have all ingredients.

We have given: a capacity of $Cap=20 \,\mu F =20\,\mu \frac{C}{V}$, a voltage of $U= 24\,V$ and a time span of $t=0,02\,s\,.$

I will use the comma as separation sign, that is I will write $\frac{1}{2}=0,5\,.$ I think we are both used to this standard and I don't want to confuse you with a point as separator (American notation). I also write $Cap$ for capacity, to avoid confusion with the $C$ for Coulomb; and $U$ for voltage, to avoid confusion with $V$ for Volt. $F$ are Farad, and $As$ Ampère times seconds.

I first calculated the load, same as you did:
$$Q=Cap \cdot U=20 \cdot \frac{\mu C}{V}\cdot 24\,V=480\mu \cdot C= 480 \cdot 10^{-6} \cdot C = 480 \cdot 10^{-6}\, A\cdot s$$
This results in a current, same as you did:
$$
I=\dfrac{Q}{t}=\dfrac{480 \mu \,As}{0,02\,s}=\dfrac{48000 \cdot 10^{-6}\,As}{2\,s}= 24000\cdot 10^{-6} \,A = 24 \cdot 10^{3}\cdot 10^{-6}\,A=24 \cdot 10^{-3}
\,A= 24\,mA
$$
And last the number of electrons, which you denoted by $x$:
$$
x=\dfrac{Q}{e}=\dfrac{480\,\mu C}{1,6\cdot 10^{-19}\, C}=\dfrac{4800}{16} \cdot 10^{-6} \cdot \dfrac{1}{10^{-19}}=300 \cdot 10^{-6+19}=3 \cdot 10^2 \cdot 10^{13}= 3\cdot 10^{15}
$$

As an additional homework, I give you this to read: https://www.physicsforums.com/insights/10-math-tips-save-time-avoid-mistakes/

I've been trying to analyze this for a while and I'm quite confused as to what exactly you did in the first equation and why you came up with μA. Is there maybe something else that i need to look up, besides the powers of 10?

 

[fresh_42]

I've been trying to analyze this for a while and I'm quite confused as to what exactly you did in the first equation and why you came up with μA. Is there maybe something else that i need to look up, besides the powers of 10?

I don't know which equation you mean. $\mu = 10^{-6}$ and you can use either of them. Originally it came from the twenty micro Farad capacity, which was given. Now as $\mu = 10^{-6}\; , \;1\,F= 1 \,C\cdot V^{-1}$ and $1\,C = 1\,A\cdot s$ we have a capacity of $Cap = 20\,\mu F = 20 \cdot 10^{-6} \cdot A \cdot s \cdot \frac{1}{V}\,.$

 

[HazyMan]

I don't know which equation you mean. $\mu = 10^{-6}$ and you can use either of them. Originally it came from the twenty micro Farad capacity, which was given. Now as $\mu = 10^{-6}\; , \;1\,F= 1 \,C\cdot V^{-1}$ and $1\,C = 1\,A\cdot s$ we have a capacity of $Cap = 20\,\mu F = 20 \cdot 10^{-6} \cdot A \cdot s \cdot \frac{1}{V}\,.$

I'm referring to the first question where you calculated the load

 

[fresh_42]

Load is capacity times voltage. Capacity is given as $20\,\mu F$ which is (see previous post) equal to $20\cdot 10^{-6}\cdot A\cdot s \cdot V^{-1}\,.$ Voltage is given as $24\,V$ so the Volt cancel in the product and we are left with $Q=20\cdot \mu \cdot F \cdot 24 \cdot V = 480\cdot \mu \cdot F\cdot V= 480 \cdot \mu \cdot A \cdot s \cdot V^{-1} \cdot V = 480\cdot 10^{-6} \cdot A \cdot s$

 

[HazyMan]

I finally managed to understand where i went wrong.
This is what i came up with. (I initially thought of taking 300x10¹³ altogether and take the 0 zeroes from the 300 and put them on the ¹³ which would give me 3x10¹⁵ but i thought it was wrong. However it realized that both methods work, but i used yours anyway.
Thanks a lot for your help!