Dot product for non-orthogonal co-ordinate systems

[Dave in NZ]

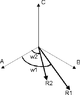
Is the result of a dot product of two vectors valid if the frame of reference unit vectors are not orthgonal?

i.e. 2D 3 axis co-ordinate system as commonly used in power systems where the axis are 120 degrees apart in 2D space?

 

[Nabeshin]

Of course. The dot product is defined independently of the basis.

 

[John Creighto]

The Dot product is the inner product. So for linear coordinates we could generalize as follows:

Let :

$$X'=UX$$

$$U^{-1}X'=X$$

$$X^TX=(X')^T((U^{-1})^TU^{-1}X'=(X')^TAX'$$

Where:

$$A=((U^{-1})^TU^{-1}$$

For non linear coordinate forms post it in the sub form dealing with tensors.

 

[Dave in NZ]

Thanks for the help, I have a follow up question:-

Does the following still apply?

(V1)(U1)+(V2)(U2)+(V3)(U3) = (R1)(R2)cos [(w1-w2)]

where V and U are the input vectors referenced to the 2D 120degree separated 3-axis co-ordinate system. R1 is the magnitude of vector V and R2 is the magnitude of vector U. w1 is the angle of R1, w2 is the angle of R2.

 

[John Creighto]

Thanks for the help, I have a follow up question:-

Does the following still apply?

(V1)(U1)+(V2)(U2)+(V3)(U3) = (R1)(R2)cos [(w1-w2)]

where V and U are the input vectors referenced to the 2D 120degree separated 3-axis co-ordinate system. R1 is the magnitude of vector V and R2 is the magnitude of vector U. w1 is the angle of R1, w2 is the angle of R2.

Let's try the derivation another way:

Call the unit bais vectors in your coordinate system b1 b2 b2.

and let's call your vectors u and v instead of w1 and w2.

Then:
$$\mbox{\boldmath u } \cdot \mbox{\boldmath v }=(u_1 \mbox{\boldmath b_1 } + u_2 \mbox{\boldmath b_2 } +u_3 \mbox{\boldmath b_3 }) \cdot (v_1 \mbox{\boldmath b_1 }+ v_2 \mbox{\boldmath b_2 } +v_3 \mbox{\boldmath b_3 })$$

$$\mbox{\boldmath u } \cdot \mbox{\boldmath v }=\sum_{i=1}^{3}\sum_{j=1}^{3}u_iv_jcos(b_i,b_j)$$

And if the coordinates are orthognal then:

$$cos(b_i,b_j)=\delta_{i,j}$$

Also regardless of the coordinate system:

$$|{\mbox{\boldmath u }|=\sqrt{\mbox{\boldmath u } \cdot \mbox{\boldmath u }}$$

 

[Dave in NZ]

Hi John, I'm rusty on notation.

Please would you expand "cos (bi,bj)"?

am I correct to assume from the special case for orthogonal unit vectors that the inner product for the non-orthgonal unit vector case is not simply R1R2cos(angle between vectors). Where R1 and R2 are the magnitudes of the two vectors?

thanks again

 

[John Creighto]

Hi John, I'm rusty on notation.

Please would you expand "cos (bi,bj)"?

I don't think it is standard notation. I just used it to represent the angle between the two unit basis vectors. The unit basis vectors are vectors of unit length and parallel to one of the axes.

am I correct to assume from the special case for orthogonal unit vectors that the inner product for the non-orthgonal unit vector case is not simply R1R2cos(angle between vectors). Where R1 and R2 are the magnitudes of the two vectors?

thanks again

If the vectors are unit vectors then their lengths R1 and and R2 are equal to one so you only care about the angle between them. Length is sometimes also called norm. The norm of w is given by:

$$|w|=sqrt(w \cdot w)=sqrt(w^Tw)$$

Note: I didn't bother using bold in this post.

 

[Dave in NZ]

Thank you John. Your explanations have been very useful. Cheers Dave

 

[John Creighto]

Thank you John. Your explanations have been very useful. Cheers Dave

Cool. What do you plant to use it for?

 

[Dave in NZ]

The phase comparator in a three phase phase-locked-loop. i.e. I've calculated the dot product of the incoming mains samples with the feedback waveform samples without doing a Clark tranform to the incoming mains samples first. The aim is to reduce computation time and keep all information, the downside is now the waveforms are not orthogonal, and hence my doubt whether the relationship between the dot product and the UVcos(u,v) holds.

The code is running in a TI DSP, but I have been getting errors I cannot account for when the incoming mains is unbalanced. Its either a calculation error or an error in the fundamental mathematics, hence the questions regarding the relationship between the dot product calculation and the commonly used polar form. I'm attempting to narrow down the options.

The overall application is a 3 phase rectifier.

 

[John Creighto]

The phase comparator in a three phase phase-locked-loop. i.e. I've calculated the dot product of the incoming mains samples with the feedback waveform samples without doing a Clark tranform to the incoming mains samples first. The aim is to reduce computation time and keep all information, the downside is now the waveforms are not orthogonal, and hence my doubt whether the relationship between the dot product and the UVcos(u,v) holds.

The code is running in a TI DSP, but I have been getting errors I cannot account for when the incoming mains is unbalanced. Its either a calculation error or an error in the fundamental mathematics, hence the questions regarding the relationship between the dot product calculation and the commonly used polar form. I'm attempting to narrow down the options.

The overall application is a 3 phase rectifier.

Ah, now I see why you didn't want to use an orthogonal basis. So, I hope that my expression for the dot product in a non orthogonal basis was clear.

 

[Dave in NZ]

to clarify would the answer for 120 degrees between unit vectors be:-

u.v = (u1)(v1)+(u2)(v2)+(u3)(v3)-(0.5)[(u1)(v2)+(u1)(v3)+(u2)(v1)+(u2)(v3)+(u3)(v1)+(u3)(v2)]

then can I assume that this is equal to:-

(u)(v)cos(angle between them)

I need the polar form to be representive as I feed what is now the scaled cosine of the phase error into the NCO to generate the feedback waveforms

 

[John Creighto]

to clarify would the answer for 120 degrees between unit vectors be:-

u.v = (u1)(v1)+(u2)(v2)+(u3)(v3)-(0.5)[(u1)(v2)+(u1)(v3)+(u2)(v1)+(u2)(v3)+(u3)(v1)+(u3)(v2)]

then can I assume that this is equal to:-

(u)(v)cos(angle between them)

I need the polar form to be representive as I feed what is now the scaled cosine of the phase error into the NCO to generate the feedback waveforms

It looks right to me to me provided that by unit vectors you mean the basis vectors for your coordinate system. It sounds like from your above post that you are doing a power application. It would make sense that if each waveform was a sine wave then the phase should be related to the angle between the waveforms.

However, if the waveforms were something else, then this wouldn't be the case.For instance, if the waveform was a pulse train then a small phase delay would cause the waveforms to be orthogonal.

 

[Dave in NZ]

The inputs (U) are sinewaves as are the feedback waveforms (V). when locked the feedback waves should lag the input waves by 90 degrees.

the three axis are 120 degrees apart. I was calling these the basis vectors.

let me know if I'm deluded :-) Thanks

 

[John Creighto]

The inputs (U) are sinewaves as are the feedback waveforms (V). when locked the feedback waves should lag the input waves by 90 degrees.

the three axis are 120 degrees apart. I was calling these the basis vectors.

let me know if I'm deluded :-) Thanks

By axis I presume you mean the inputs waveforms. You actually only have two linearly independent basis vectors since any sine wave can be represented as the sum of a sine wave and a cosine wave.

That said you can still represent the wave using an over determined set of basis vectors if you wish. My guess is somehow you know how to represent the feedback waveform in terms of a sum of the input vectors.

P.S. is your company hiring? It sounds like you are doing interesting work. Or is it just a school research project?

 

[Dave in NZ]

Hi John, This is a commerical product. The work is interesting and challenging. We have just "released" just under 10% of our staff globally so chances of a job are low but you are welcome to apply:-
LOCAL SITE
http://www.powerware.co.nz/New_Zealand/careers/default.asp
GLOBAL SITE
http://www.eaton.com/EatonCom/OurCompany/Careers/index.htm