- #1
odolwa99
- 85
- 0
In the final proof, I have [itex]\frac{h-h\tan B}{\tan B}[/itex], rather than [itex]\frac{h-h\tan B}{1+\tan B}[/itex]. Can anyone help me out?
Many thanks.
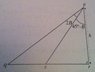
In the triangle pqr (see attachment), [itex]|\angle qrp|=90^{\circ}[/itex] & |rp| = h. s is a point on [qr] such that [itex]|\angle spq|=2B[/itex] & [itex]|\angle rps|=45^{\circ}-B[/itex], [itex]0^{\circ}<B<45^{\circ}[/itex]. Show that [itex]|sr|=h \tan(45^{\circ}-B)[/itex]
[itex]h\tan(45-B)=h(\frac{\tan45-\tan B}{1+ tan45\cdot\tan B})=\frac{h-h\tan B}{1+\tan B}[/itex]
Apply the sine rule: [itex]\frac{\sin(45-B)}{|sr|}=\frac{\sin(180-(90+45-B))}{h}[/itex]
[itex]h(\sin(45-B))=|sr|\sin(45+B)[/itex]
[itex]h(\sin\cos B-\cos45\sin B)=|sr|(\sin45\cos B+\cos45\sin B)[/itex]
[itex]h(\frac{\cos B}{\sqrt{2}}-frac{sin B}{\sqrt{2}})=|sr|(\frac{\cos B}{\sqrt{2}}+\frac{\sin B}{\sqrt{2}})[/itex]
[itex]|sr|=(\frac{h\cos B-h\sin B}{\sqrt{2}})/(\frac{\cos B}{\sin B}{\sqrt{2}})[/itex]
[itex]\frac{h\sqrt{2}(\cos B- \sin B)}{\sqrt{2}(\cos B+\sin B})[/itex]
[itex]h(\frac{\sin B}{\cos B}+\frac{\cos B}{\sin B})[/itex]
[itex]h(-\tan B+\frac{1}{\tan B})[/itex]
[itex]\frac{h-h\tan B}{\tan B}[/itex]
Many thanks.
Homework Statement
In the triangle pqr (see attachment), [itex]|\angle qrp|=90^{\circ}[/itex] & |rp| = h. s is a point on [qr] such that [itex]|\angle spq|=2B[/itex] & [itex]|\angle rps|=45^{\circ}-B[/itex], [itex]0^{\circ}<B<45^{\circ}[/itex]. Show that [itex]|sr|=h \tan(45^{\circ}-B)[/itex]
Homework Equations
The Attempt at a Solution
[itex]h\tan(45-B)=h(\frac{\tan45-\tan B}{1+ tan45\cdot\tan B})=\frac{h-h\tan B}{1+\tan B}[/itex]
Apply the sine rule: [itex]\frac{\sin(45-B)}{|sr|}=\frac{\sin(180-(90+45-B))}{h}[/itex]
[itex]h(\sin(45-B))=|sr|\sin(45+B)[/itex]
[itex]h(\sin\cos B-\cos45\sin B)=|sr|(\sin45\cos B+\cos45\sin B)[/itex]
[itex]h(\frac{\cos B}{\sqrt{2}}-frac{sin B}{\sqrt{2}})=|sr|(\frac{\cos B}{\sqrt{2}}+\frac{\sin B}{\sqrt{2}})[/itex]
[itex]|sr|=(\frac{h\cos B-h\sin B}{\sqrt{2}})/(\frac{\cos B}{\sin B}{\sqrt{2}})[/itex]
[itex]\frac{h\sqrt{2}(\cos B- \sin B)}{\sqrt{2}(\cos B+\sin B})[/itex]
[itex]h(\frac{\sin B}{\cos B}+\frac{\cos B}{\sin B})[/itex]
[itex]h(-\tan B+\frac{1}{\tan B})[/itex]
[itex]\frac{h-h\tan B}{\tan B}[/itex]