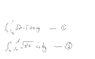- #1
engineer_dave
- 35
- 0
Homework Statement
Evaluate the integral shown in the diagram
Homework Equations
The Attempt at a Solution
The first step to evaluating the integral is shown in the diagram (labelled as 2). They said they changed the order of integration. I was wondering what they mean by changing the order of integration and how did they come up with that first step. Cheers!