- #1
Like Tony Stark
- 179
- 6
- Homework Statement
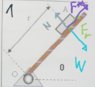
- The picture shows a block on an arm. This arm is rotating with constant angular velocity. There is friction between the block and the arm, and the block is about to slide down.
- Relevant Equations
- Newton's equations
I know that, if my ##X## axis is aligned with the arm, there is friction pointing to ##O## and the ##x## component of the weight. Then, on the ##Y## axis, there is the normal force and the ##y## component of the weight.
Supposing that I am situated on the arm (non inertial frame), where is the centrifugal force pointing to? Because, if I think the problem as a spinning ball, the centrifugal force is aligned with the tension, so in this case this pseudo-force would be in the ##x## axis. But if I think as if I were on the arm, I think that I would feel pushed against the arm, so the centrifugal force would be in the ##y## axis.
What's the correct option?
Supposing that I am situated on the arm (non inertial frame), where is the centrifugal force pointing to? Because, if I think the problem as a spinning ball, the centrifugal force is aligned with the tension, so in this case this pseudo-force would be in the ##x## axis. But if I think as if I were on the arm, I think that I would feel pushed against the arm, so the centrifugal force would be in the ##y## axis.
What's the correct option?