- #1
frozen7
- 163
- 0
https://www.physicsforums.com/attachment.php?attachmentid=4225&stc=1
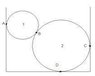
Determine the reaction forces at the four contact points A,B,C,D. The hollow balls which are homogenous and made of the same material have masses of 1.02kg and 2.04kg and the chamber they sit in is 55.98cm wide. Everything is smooth,so that the friction is negligible.
Can anyone help me in this question?
Determine the reaction forces at the four contact points A,B,C,D. The hollow balls which are homogenous and made of the same material have masses of 1.02kg and 2.04kg and the chamber they sit in is 55.98cm wide. Everything is smooth,so that the friction is negligible.
Can anyone help me in this question?