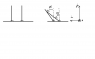- #1
BrBa
- 1
- 0
Homework Statement
Two rigid bars of equal length, masses m1 and m2, and inertias I1 and I2 are initially upright and separated by a distance d. The rods can be assumed to be pinned to the ground such that they are free to have angular rotation. The bar on the right (2) is given an infinitesimal push to the left so that it is set into motion and impacts the bar on the left (1). Upon colliding assume that there is no rebound of bar 2 and it slides without friction along bar 1 as the two fall.
Determine all the equations of motion. Find the reactions at pins.
Homework Equations
ma = Ʃ Forces
conservation of angular momentum
d/dt (I ω) = ƩMoments
Kinematic equations of rigid bodies
Vg = Va + ω x r(ag) , etc.
The Attempt at a Solution
One has to analyze the system in 3 parts, before impact, during impact, and after impact. All I know so far is that for before:
ΔPE + ΔKE = 0
mg(L/2)sin(θ) = 1/2 I(2)ω^2
I = m(2)L^2 / 3
Thus,
ω(2)- = √3gsinθ/L in the k direction
and ω(1)- = 0 k because there is no contact yet.
where the "-" indicated before impact.