- #1
Ghost117
- 50
- 3
This is part of a question from Griffiths 4.5 (electrodynamics, 4th edition)
p1 and p2 are (perfect) dipoles a distance r apart (Their alignment is such that p1 is perpendicular to the line separating them (pointing upwards) and p2 is parallel to the line separating them (pointing away from p1).)
What is Field of p1 at p2, and the Field of p2 at p1?
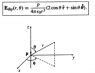
Edip(r,θ) = p/(4πε0r3) * (2cosθr + sinθθ)
I actually have the official solution for this, but I don't understand it... The theta value in the solution uses theta = π/2 for the field of p1 at p2, but a value of theta = π, for the equation for p2 at p1.. And I don't see where either of these theta values are coming from (my spherical coordinates are very weak, and I suspect that's the real problem here.)
Thanks
Homework Statement
p1 and p2 are (perfect) dipoles a distance r apart (Their alignment is such that p1 is perpendicular to the line separating them (pointing upwards) and p2 is parallel to the line separating them (pointing away from p1).)
What is Field of p1 at p2, and the Field of p2 at p1?
Homework Equations
Edip(r,θ) = p/(4πε0r3) * (2cosθr + sinθθ)
The Attempt at a Solution
I actually have the official solution for this, but I don't understand it... The theta value in the solution uses theta = π/2 for the field of p1 at p2, but a value of theta = π, for the equation for p2 at p1.. And I don't see where either of these theta values are coming from (my spherical coordinates are very weak, and I suspect that's the real problem here.)
Thanks