- #1
HAMJOOP
- 32
- 0
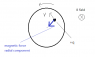
A conducting disk is rotating under a uniform magnetic field.
Using Lorentz force F = qv x B, we can conclude that emf produced.
Using Faraday's law, ∫E dl = 0 for any closed loops since there is no magnetic flux change.
So E = 0.
Contradiction ?
Using Lorentz force F = qv x B, we can conclude that emf produced.
Using Faraday's law, ∫E dl = 0 for any closed loops since there is no magnetic flux change.
So E = 0.
Contradiction ?