Eectrodynamics-neutral points?

[humanist rho]

Homework Statement

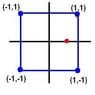
If 4 charges are kept fixed in 4 corners of a square,how many points are inside the square where the field vanishes?


2. The attempt at a solution

The central point is a neutral point because the net force is zero there. I want to know whether there's any other neutra point?

 

[ehild]

What about the magnitude and sign of the charges? Are they all equal? ehild

 

[humanist rho]

What about the magnitude and sign of the charges? Are they all equal?


ehild

yes.equal charges of same sign.

 

[humanist rho]

Please help.
Theres more neutral points in the system. But how can i locate them?

 

[ehild]

See the picture. Try to locate the point along the diagonal.

ehild

 

[humanist rho]

I think,to locate neutral point the net field due to 4 charges should be found and equated to zero.

At the point shown in figure , field due to the two diagonally opposite charges is $$\frac{q}{x^{2}}+\frac{q}{(a√2-x)^{2}}$$,a is the side of square.


How to find the field due to other two charges at the point or do they cancel each other?

 

[ehild]

Do not forget that the electric field is a vector. It has direction. So your formula is not correct. What is the contribution of the electric field due to the nearest charge and what is it from the other charge on the same diagonal?
As for the other charges, find their distance from the red point. Also find the direction of their electric field. Draw the electric field vectors into the picture. What are the horizontal and vertical components?

ehild

 

[humanist rho]

Net field,$$E = \frac{1}{4\pi \in _{0}}\left\{ \frac{q}{\left( a\sqrt{2}% -x\right) ^{2}}\hat{x}-\frac{q}{x^{2}}\hat{x}+\frac{q\left[ \left( \frac{a}{% \sqrt{2}}-x\right) \hat{x}+\frac{a}{\sqrt{2}}\hat{y}\right] }{\left[ \left( \frac{a}{\sqrt{2}}-x\right) ^{2}+\frac{a^{2}}{2}\right] ^{3/2}}+\frac{q\left[ \left( \frac{a}{\sqrt{2}}-x\right) \hat{x}-\frac{a}{\sqrt{2}}\hat{y}\right] }{\left[ \left( \frac{a}{\sqrt{2}}-x\right) ^{2}+\frac{a^{2}}{2}\right] ^{3/2}}\right\}$$

The y components cancel.

$$ie,E=\frac{1}{4\pi \in _{0}}\left\{ \frac{q}{\left( a\sqrt{2}% -x\right) ^{2}}\hat{x}-\frac{q}{x^{2}}\hat{x}+\frac{2q\left( \frac{a}{\sqrt{2% }}-x\right) }{\left[ \left( \frac{a}{\sqrt{2}}-x\right) ^{2}+\frac{a^{2}}{2}% \right] ^{3/2}}\hat{x}\right\}$$

On equating to zero,

$$\left[ \left( \frac{a}{\sqrt{2}}-x\right) ^{2}+\frac{a^{2}}{2}\right] ^{3/2}x^{2}-\left( a\sqrt{2}-x\right) ^{2}\left[ \left( \frac{a}{\sqrt{2}}% -x\right) ^{2}+\frac{a^{2}}{2}\right] ^{3/2}+2q\left( \frac{a}{\sqrt{2}}% -x\right) \left( a\sqrt{2}-x\right) ^{2}x^{2}=0$$


Am i complicating things?(i usually do so :) )

 

[ehild]

Well, it is not that complicated if you use other notations, but I can not find a proper root which is inside the square.

ehild

 

[ehild]

I asked the other HH-s, and they found neutral points along the bisectors of the sides.
Write up the equation for the electric field and type into wolframalpha.com to get the solutions. No need to use a or a/2 for the sides of the square, use the coordinates as they are in the figure.

ehild

 

[humanist rho]

Still i didn't get it. :(

I chose the red point as (x,0)

Then my euations are,

$$E=\frac{q}{4\pi \varepsilon _{0}}\left[ \frac{[(x+1)\hat{x}-\hat{y}]}{% [(x+1)^{2}+1]^{3/2}}+\frac{[(x+1)\hat{x}+\hat{y}]}{[(x+1)^{2}+1]^{3/2}}+% \frac{(x-1)\hat{x}+\hat{y}}{[(x-1)^{2}+1]^{3/2}}+\frac{(x-1)\hat{x}-\hat{y}}{% [(x-1)^{2}+1]^{3/2}}\right]=0$$

$$\frac{q}{4\pi \varepsilon _{0}}\left[ \frac{2(x+1)\hat{x}}{% [(x+1)^{2}+1]^{3/2}}+\frac{2(x-1)\hat{x}}{[(x-1)^{2}+1]^{3/2}}\right]=0$$

$$(x+1)[(x-1)^{2}+1]^{3/2}+(x-1)[(x+1)^{2}+1]^{3/2}=0$$

In wolfram alpha the solutions are 0,and two imaginary numbers.

 

[humanist rho]

Sorry, i got it.
On approximating the solutions i got neutral points near ±0.7.

solution

At last i conclude that there are four neutral points.

Thank you very much for your time and effort,sir.

 

[ehild]

Sorry, i got it.
On approximating the solutions i got neutral points near ±0.7.

solution

Then can i conclude that there are 4 neutral points?

Congrats! There are five of them, including the centre.
Do not forget, that the ±0.7 is ±0.7 a/2 if the side of the square is a.
It can be shown that the neutral point must be in the plane of the square and on a symmetry element. But it appeared that the diagonal was not right.

It is easier to write up such problems in therms of the potential and plotting it out, looking for places where the gradient is zero.
If you plot the potential along one bisector, it has a minimum at the centre and maximums at about ±0.7.
In case of a diagonal, there is a broad minimum in the centre, and then the potential increases in both direction.

That was a challenging problem! And the solution was not mine, but of the other Homework Helpers: Vela, Gneill (he made a very nice picture, ask him to show it to you) Vanadium 50.

ehild

 

[humanist rho]

Hats off to them also.You all simply rock!

 

[biswajitdalal]

what is the exact calculation for his problem? please post it and also give the clear diagram about the potential.