- #1
judas_priest
- 174
- 0
Homework Statement
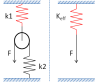
What is the effective spring constant for the system of the two springs, perfect pulley, and string shown on the left for it to be modeled by just one spring (constant keff) as shown on the right?
Homework Equations
The Attempt at a Solution
With k2 getting stretched by D, the pulley goes down by 2D. Therefore,
x1 = F/k1, x2 = F/k2
x1 + 2(x2) = F/k1 + 2F/k2
Solving this, I get k effective as
(2*k1*k2)/(k2+2*k1)
But this doesn't match the given answer. Where am I going wrong?