How to Find R from Electric Charge Problem

In summary, the equation given to find the distance between charges does not work correctly because the x-component of the force is not taken into account.
  • #1
kidi3
26
0

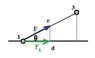
Homework Statement



http://snag.gy/Zg3SO.jpg
At the moment is it question A


The Attempt at a Solution


A)
I've realized that Force applied by F_31 + F_41 = F_21

SO I've writte this equation up but Mathmathica, says there is an errror, and gives me an incorrect result.

http://snag.gy/rQ2kz.jpg

Mathmatica says it should {{D -> -0.225008}, {D -> 0.185008}}

The correct answer should be 2,27cm.
 
Physics news on Phys.org
  • #2
Did you take into account the directions of the forces F_31 and F_41? They have both x and y components. :smile:
 
  • #3
No..
y -component must be zero since it is zero for q2
and the sum of q3 and q4 would negate the y component.
 
  • #4
kidi3 said:
No..
y -component must be zero since it is zero for q2
and the sum of q3 and q4 would negate the y component.

Correct. So, you only need to work with the x components of the forces.
 
  • #5
But aren't I doing it already?
 
  • #6
kidi3 said:
But aren't I doing it already?

I don't think so. It appears to me that on the left hand side of http://snag.gy/rQ2kz.jpg you are using the full magnitude of the forces F_31 and F_41, rather than their x-components.
 
  • #7
Ahh.. so you want me to skip
d/cos([itex]\theta[/itex])
and just use d.. ?
 
Last edited:
  • #8
kidi3 said:
Ahh.. so you want me to skip
d/cos([itex]\theta[/itex])
and just use d.. ?

No, that part is correct, r = d/cosθ is the correct distance between charges 4 and 1. Draw a sketch showing the direction of the force F41. How would you express the x-component of F41 in terms of F41 and θ?
 
  • #9
well the distance it moves is d.. so I have to write an expression for d..

So it would be rcosθ = d??
 
  • #10
Sorry, but I don't understand. What is moving a distance d? I thought you were trying to find the distance D so that the net force on q1 is zero.

Your first equation which you derived looks good except it doesn't take into account that you want the x-components of the forces to add to zero. (You already know the y-components add to zero by symmetry.)
 
  • #11
well q1 lies on a distance d from q3 and q4...

and isn't that distance given by r cos(θ)= d

where r is the Hypotenuse of the triangle`..
 
  • #12
kidi3 said:
well q1 lies on a distance d from q3 and q4...

and isn't that distance given by r cos(θ)= d

where r is the Hypotenuse of the triangle`..

Yes. All of that is correct. So, your expression (d/cosθ)2 in the denominator of your equation is correct. :smile:

Force is a vector quantity. The equation F = q1q2/(4∏εor2) gives the magnitude of the force. You need to determine the x-component of the force vector. Again, a sketch of the forces will help.
 
  • #13
... hmm would it then be
F_x = q1q2/(4∏εo(d))

Since both lies in a distance d?... or how..
 
  • #14
kidi3 said:
... hmm would it then be
F_x = q1q2/(4∏εo(d))

Since both lies in a distance d?

No. Consider the x-component of F31. Can you use trigonometry or similar triangles to find Fx in the attached picture?
 

Attachments

  • Force component.jpg
    Force component.jpg
    4.1 KB · Views: 363
  • #15
hmmm.. is it then cos(\theta)=r/x <=> x = cos(theta)/r
 
  • #16
kidi3 said:
hmmm.. is it then cos(\theta)=r/x <=> x = cos(theta)/r

Not sure what you are writing here. You need to find Fx, rather than x.
 
  • #17
Ahh.. I see what you mean now..
My drawings weren't correct..
But by using youre drawing I see that Cos(theta) = F_x/F <=> F_x = Fcos(theta)

So the expression for F_X = (q1q2/(4∏εo(d^2))) cos(theta)
 
  • #18
Yes. Good.

[EDIT: oops, you did mean r instead of d in the denominator, right? And the charges are q1 and q3 ]
 
Last edited:
  • #19
Hmm.. but i still get an incorrect answer.. :(

http://snag.gy/LDwAe.jpg

When i Tries to calculate D i get complex number..
 
  • #20
It seems to work out ok. Note that you don't want to plug in a negative value for q3 since you have set up your equation to state that the magnitudes of the forces balance out.
 
  • #21
D has to be 2,266 cm
But i get 1471,4 m...
 
  • #22
Well, I get D = 1.92 cm. :frown:

If you go to your original equation, put in the cosθ factor on the left to get the x-component, and then simplify, see if you get

2q3cos3θ/d2 = q2/R2

where I let R be the total distance between 1 and 2.

If so, what do you get if you solve for R?
 
  • #23
How do you get this ?
2q3cos3θ/d2 = q2/R2
 
  • #24
Well, what do you get if you cancel out everything you can between the left and right hand sides?
 
  • #25
But isn't what i have already done before..
 
  • #26
I don't know. You really haven't shown any steps involved in solving your equation. So, I can't tell you were you are going wrong.
 
  • #27
Start with your original equation and put in a factor of cosθ on the left side to take care of getting the x-component.

Then, do you see that q1 cancels out as well as 4πεo?

For now, just let r stand for the distance between #3 and #1 charge. So, instead of writing d/cosθ on the left, just write r. And on the right side, let R be the total distance between #2 and #1. So, instead of writing D+d just write R. Can you state what the equation simplifies to?
 
  • #28
These are my steps...

http://snag.gy/3oGJ5.jpg
 
  • #29
The first equation is incorrect. I see you have the cosθ factor to get the x-component. Good. But for some reason you forgot to write (d/cosθ)2 in the denominator to represent r2.
 
  • #30
Also looks like you didn't go from the second to the third equation correctly. [Shouldn't the fraction inside the square root be flipped over?]
 
  • #31
#30
Well.. would it make any difference?
#29
yeah i may have understood your previous post..
Now is the result
1.89577

http://snag.gy/E71gm.jpg
 
  • #32
kidi3 said:
#30
Well.. would it make any difference?
#29

Yes. The big fraction in the square root is upside down.
 
  • #33
...'
I still get an incorrect answer..

http://snag.gy/veJcm.jpg
 
  • #34
It's not the d/cosθ that should be flipped. When you got down to your last expression with the square root, the main fraction inside the square root appears to be upside down (not the d/cosθ).

For the moment, let's let r = d/cosθ and R = d+D

Then your original equation can be written as

2q3cosθ/r2= q2/R2

What does this become if you multiply both sides by r2R2?
 
  • #35
I am getting confused.. wasn't F_x i shoud have used..

And the error, I really don't understand how there can be a error in the equation i wrote..
 
<h2>1. How do I calculate the value of R from an electric charge problem?</h2><p>To find the value of R in an electric charge problem, you can use the formula R = Q/V, where Q is the electric charge and V is the potential difference. This formula is known as Ohm's Law and is commonly used in circuit analysis.</p><h2>2. What units should I use for R in an electric charge problem?</h2><p>The unit for R is ohms (Ω), which is the standard unit for electrical resistance. It is important to use the correct units in any calculation to ensure accurate results.</p><h2>3. Can I use the same formula to find R in both AC and DC circuits?</h2><p>Yes, the formula R = Q/V can be used in both AC (alternating current) and DC (direct current) circuits. However, in AC circuits, the value of R may vary depending on the frequency of the current.</p><h2>4. Is there a way to find R if I only know the value of current?</h2><p>Yes, you can use Ohm's Law in its alternative form, R = V/I, where V is the potential difference and I is the current. This formula can be used to find R if you only know the current and potential difference in a circuit.</p><h2>5. What is the significance of R in an electric charge problem?</h2><p>R, or resistance, is a crucial component in any electric circuit. It determines the amount of current that can flow through a circuit for a given potential difference. It also helps regulate the flow of electricity and prevents damage to devices by limiting the current.</p>

1. How do I calculate the value of R from an electric charge problem?

To find the value of R in an electric charge problem, you can use the formula R = Q/V, where Q is the electric charge and V is the potential difference. This formula is known as Ohm's Law and is commonly used in circuit analysis.

2. What units should I use for R in an electric charge problem?

The unit for R is ohms (Ω), which is the standard unit for electrical resistance. It is important to use the correct units in any calculation to ensure accurate results.

3. Can I use the same formula to find R in both AC and DC circuits?

Yes, the formula R = Q/V can be used in both AC (alternating current) and DC (direct current) circuits. However, in AC circuits, the value of R may vary depending on the frequency of the current.

4. Is there a way to find R if I only know the value of current?

Yes, you can use Ohm's Law in its alternative form, R = V/I, where V is the potential difference and I is the current. This formula can be used to find R if you only know the current and potential difference in a circuit.

5. What is the significance of R in an electric charge problem?

R, or resistance, is a crucial component in any electric circuit. It determines the amount of current that can flow through a circuit for a given potential difference. It also helps regulate the flow of electricity and prevents damage to devices by limiting the current.

Similar threads

Getting electric potential from charge density over whole sp
    • Advanced Physics Homework Help
Replies
1
Views
999
Electric field of "half" an infinite charged sheet
    • Advanced Physics Homework Help
Replies
1
Views
1K
Calculate electric polarizability
    • Advanced Physics Homework Help
Replies
1
Views
803
Dipole of charge distribution
    • Advanced Physics Homework Help
Replies
1
Views
1K
Electric field external to Conducting Hollow Sphere with charge inside
    • Introductory Physics Homework Help
Replies
17
Views
400
Sphere-with-non-uniform-charge-density ρ= k/r
    • Advanced Physics Homework Help
Replies
8
Views
7K
Electric field of a charged dielectric sphere
    • Advanced Physics Homework Help
2
Replies
37
Views
10K
Charge on a grounded conducting sphere in a uniform electric field, after ungrounding and movement
    • Introductory Physics Homework Help
Replies
1
Views
144
I Do Electric field lines propagate by themselves away from a charge?
    • Electromagnetism
3
Replies
73
Views
3K
Find the magnitude of the electric force from 3 charges at vertices of a cube
    • Introductory Physics Homework Help
Replies
17
Views
982

Hot Threads

Recent Insights

Back
Top