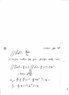- #1
yoni162
- 16
- 0
Homework Statement
We have a sphere with radius b, within that sphere there's another sphere with radius a. Between the two spheres we have an electric charge with density A/r. Also, we have a charge Q in the center. We need to find the constant A so that the field between a and b is independent of r (meaning, it's constant for a<=r<=b).
Homework Equations
Gauss' law.
The Attempt at a Solution
I added the scanned pages I've written, it should be understandable. As I said, I used Gauss' law to calculate the field, using a sphere with radius r (a<=r<=b) to calculate the electric flux. After finding the electric field as a function of r, I calculated d(E(r))/dr and demanded that it would be=0, but I can't seem to get a solution for A that's independent of r.