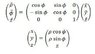Flux through a Disk: What's Wrong with My Method?

[roam]

Homework Statement

According to my textbook, the electric flux through a disk of radius R situated at a height d from the xy plane is given by:

$2 \pi k_0 Q [1- \frac{d}{\sqrt{R^2+d^2}}]$

Where $k_0 = \frac{1}{4\pi \epsilon_0}$

I'm having some difficulty obtaining this answer.

Homework Equations

Coulomb's law.

Flux $\Phi = E A$

Where A is the area of the disk, in this case $A=\pi R^2$.

The Attempt at a Solution

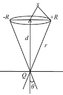
I've attached a diagram I made of the method I am using here:

So $cos \theta = z/r$, $r=\sqrt{d^2+x^2}$ (x runs from 0 to R):

$E= \frac{1}{4 \pi \epsilon_0} \int^R_0 \frac{2Qd}{(d^2+x^2)^{3/2}} \implies \frac{1}{4 \pi \epsilon_0} \frac{2QR}{d \sqrt{d^2+R^2}}$

Now, the flux is the product:

$\Phi = \frac{1}{4 \pi \epsilon_0} \frac{2QR}{d \sqrt{d^2+R^2}} \pi R^2 = 2 \pi k_0 Q \left( \frac{R^3}{d\sqrt{d^2+R^2}} \right)$

So why does my answer not match the one in the book? What's wrong with my method, and how can I get the correct solution?

Any help is greatly appreciated.

 

[BvU]

Good thing you posted the picture -- otherwise we wouldn't have known this is about a charge Q at the origin ...


With flux $\Phi = E A$ you of course mean the vector product $d\Phi(r, \phi, d) = \vec E(r, \phi, d) \cdot \vec {dA}(r,\phi)$, I hope ?

You do want to make that a lot clearer, especially to yourself. Also in the picture (drawing x at R is an unfortunate choice !)

Since there is no $\phi$ component of $\vec E$ (but there is an r component of $\vec E$ ! Fortunately it cancels when integrating over $\phi$) this simplifies to $d\Phi(r,d) = \vec E_z \; 2\pi r dr$ and now you can integrate from r = 0 to r = R.

Spoiler

Ashish Arora does it all for you here or -- with a different voice -- here

 

[roam]

Good thing you posted the picture -- otherwise we wouldn't have known this is about a charge Q at the origin ...With flux $\Phi = E A$ you of course mean the vector product $d\Phi(r, \phi, d) = \vec E(r, \phi, d) \cdot \vec {dA}(r,\phi)$, I hope ?

You do want to make that a lot clearer, especially to yourself. Also in the picture (drawing x at R is an unfortunate choice !)

Since there is no $\phi$ component of $\vec E$ (but there is an r component of $\vec E$ ! Fortunately it cancels when integrating over $\phi$) this simplifies to $d\Phi(r,d) = \vec E_z \; 2\pi r dr$ and now you can integrate from r = 0 to r = R.

Spoiler

Ashish Arora does it all for you here or -- with a different voice -- here

Thank you very much for your reply and the link. I have a follow up question. I am asked to find the flux through the disk as $R \to \infty$. How do we do that?

Since we had:

$\Phi = 2 \pi k_0 R \left( 1- \frac{d}{R^2+d^2} \right)$

Clearly, as R tends to $\infty$, the denominator $\sqrt{R^2+d^2}$ gets larger. So that means the electric flux apparently increases?

Is there something one can do mathematically to justify this further?

 

[BvU]

Misread again. What you write isn't the expression for $\Phi$ ?

 

[roam]

Misread again. What you write isn't the expression for $\Phi$ ?

What do you mean? Yes, $\Phi$ represents flux through the surface, and in this case it's given by:

$\Phi = 2\pi k_0 R (1-\frac{d}{\sqrt{d^2+R^2}})$

 

[BvU]

In post #1 it was $$
2 \pi k_0 Q [1- \frac{d}{\sqrt{R^2+d^2}}]
$$which does have a dimension of flux.

And for big enough R it goes to $Q\over 2\epsilon_0$ which is half the total flux. As can be expected.

 

[roam]

In post #1 it was $$
2 \pi k_0 Q [1- \frac{d}{\sqrt{R^2+d^2}}]
$$which does have a dimension of flux.

And for big enough R it goes to $Q\over 2\epsilon_0$ which is half the total flux. As can be expected.

Yes, it's very clear now. Thank you very much.

Here's my last question. I was told that it's better to use cylindrical coordinates for this problem to exploit the symmetry. Is it possible to derive this expression for flux, but using cylindrical polar coordinates instead?

Here's my attempt:

First I need to write the electric field in polar form:

$\hat{E} = \frac{1}{4 \pi \epsilon_0} \frac{Q}{r^2} \hat{r}$ ...(1)

Since $\hat{r}$ is a unit vector, it can be written as $r/||r||$. So (1) becomes:

$\hat{E} = \frac{1}{4 \pi \epsilon_0} \frac{Q}{r_x^2+r_y^2+r_z^2} \frac{r_x+r_y+r_z}{\sqrt{r_x^2+r_y^2+r_z^2}}$

Since this has length 1 I think we can just use unit vectors $\hat{x}, \hat{y}, \hat{z}$ on the numerator so:

$\hat{E} = \frac{Q}{4 \pi \epsilon_0} \frac{\hat{x}+ \hat{y}+ \hat{z}}{(r_x^2+r_y^2+r_z^2)^{3/2}}$

Using the transformation matrices I've attached, we find the following to substitute in:

$x= \rho cos \phi, \ y = \rho sin \phi, z=z$ and

$\hat{\rho}= cos \phi \hat{x} + sin \phi \hat{y}$
$\hat{\phi}= -sin \phi \hat{x} + cos \phi \hat{y}$
$\hat{z} = \hat{z}$

Substituting:

$\hat{E} = \frac{Q}{4 \pi \epsilon_0} \frac{(cos \phi - sin \phi)\hat{x}+ (sin \phi + cos \phi) \hat{y}+ \hat{z}}{(\rho^2 cos^2 \phi)+\rho^2 sin^2 \phi+z^2)^{3/2}}$

As before we can substitute this into:

$d \Phi = E.ds \ cos \theta$

Is this the way to go? Or do I need to drop the $cos \theta$ term and do something like a triple integral $\int^{2\pi}_{0} \int^R_0 \int^{d}_0 dz d \rho d\phi$)?

 

[roam]

Oops, I made a mistake in my post above. I just converted the $\hat{x}, \hat{y}, \hat{z}$ so:

It still seems a bit messy to integrate... Is it correct now? So, basically I need to integrated this as mentioned in my last post?

 

[BvU]

You're making this complicated ! Post #2 already was expressed in cylindrical coordinates .

Messy is relative. Once you remember that $\sin^2+\cos^2=1$ it simplifies. And think what you want to do with the $\rho$ component: for every point on the disc it is pointing in another direction !


And what is meant with "$d \Phi = E.ds \ cos \theta$" ? There is a dot in there, but do you mean dot product ? Or |E| |ds| cosϑ ?
(What I called $\vec E(r, \phi, d) \cdot \vec {dA}(r,\phi)$ in #2).

You worry me when you mention a triple integral. Flux has to do with surface, a 2D beast. There definitely is no integral $\int_0^d dz$ !
(And, by the way, $dxdydz$ is not equal to $d\rho d\phi dz$ ! -- just check the dimensions to see that that can't be right !)

 

[roam]

You're making this complicated ! Post #2 already was expressed in cylindrical coordinates .

Messy is relative. Once you remember that $\sin^2+\cos^2=1$ it simplifies. And think what you want to do with the $\rho$ component: for every point on the disc it is pointing in another direction !And what is meant with "$d \Phi = E.ds \ cos \theta$" ? There is a dot in there, but do you mean dot product ? Or |E| |ds| cosϑ ?
(What I called $\vec E(r, \phi, d) \cdot \vec {dA}(r,\phi)$ in #2).

You worry me when you mention a triple integral. Flux has to do with surface, a 2D beast. There definitely is no integral $\int_0^d dz$ !
(And, by the way, $dxdydz$ is not equal to $d\rho d\phi dz$ ! -- just check the dimensions to see that that can't be right !)

Oh, thank you so much! It didn't occur to me to use that identity!

In fact, the 'dxdydz' bit was a typo. So it should become:

$\vec{E} = \frac{Q}{4 \pi \epsilon_0} \frac{\rho \hat{\rho} + z \hat{z}}{\rho^2 +z^2}$

$\Phi = \int d \Phi = \frac{Q}{4 \pi \epsilon_0} \int_0^{2\pi} \int_0^R \frac{\rho \hat{\rho} + z \hat{z}}{\rho^2 +z^2} d\rho d\phi$

Is this alright, or do I need to use the form $\frac{sin \phi \hat{\rho}+ cos \phi \hat{z}}{\rho^2 +z^2}$?

 

[BvU]

Now you write it as if $d\Phi = \vec {dE}$ -- you equate a scalar to a vector !? And what are you integrating over ?

And there was a 3/2 power in the denominator that got lost ...