Electric Flux and Charge Distribution in a Cube with Uniform Electric Fields

[Bashyboy]

Homework Statement

Hello, the problem I am working on is:

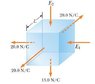
Assume the magnitude of the electric field on each face of the cube of edge L = 1.05 m in the figure below is uniform and the directions of the fields on each face are as indicated. (Take E1 = 31.5 N/C and E2 = 26.5 N/C.)

(a) Find the net electric flux through the cube.

(b) Find the net charge inside the cube.

(c) Could the net charge be a single point charge?

I attached the diagram in my post.

Homework Equations

The Attempt at a Solution

I was able to answer all but part (c) properly. I answered yes. Is it false because there aren't any electric field lines flowing out from the cube through one of the surfaces?

 

[TSny]

The electric field is given to be uniform over each face. Can you think of any way that a single point charge could produce a uniform field over a flat surface?

 

[Bashyboy]

Well, if the point charge was placed at the geometric center, wouldn't the same amount of electric field lines emanating from the point charge go through each face?

 

[TSny]

Well, if the point charge was placed at the geometric center, wouldn't the same amount of electric field lines emanating from the point charge go through each face?

Yes, the flux would be the same for each face. But I don't see how that helps. For your problem, the flux is not the same through each face.

In your problem, each face has an electric field that is perpendicular to the face and has constant magnitude over the face. Can this be achieved with a single point charge inside?

Actually, you would be allowed to set up any charges anywhere outside the cube without affecting the net charge inside. So, the question is whether or not you could arrange charges outside the cube along with a single point charge inside to produce the given uniform fields at each face of the cube.

 

[Bashyboy]

Oh, I see. If it were a point contained at the geometric center, there would be more than one electric field line passing through each face, and some of them would be at an angle less than 90 deg., relative to the face that that electric field line is passing through. Is that correct?

 

[TSny]

Oh, I see. If it were a point contained at the geometric center, there would be more than one electric field line passing through each face, and some of them would be at an angle less than 90 deg., relative to the face that that electric field line is passing through. Is that correct?

That's right. The field of a point charge could not be perpendicular to to a flat surface at each point of the surface.

 

[Bashyboy]

Why can't there be exactly one electric field line on each face that is perpendicular to it? I know the rest of the electric field lines will be at different angles, but it seems like at least one would be.

 

[TSny]

The picture that you posted is just indicating the direction of the electric field at each face. It does not mean that there is only one electric field line for each face. If you were to draw the electric field lines at the left face, for instance, then you would draw a number of parallel field lines equally spaced and perpendicular to the face.

 

[Bashyboy]

The picture that you posted is just indicating the direction of the electric field at each face. It does not mean that there is only one electric field line for each face. If you were to draw the electric field lines at the left face, for instance, then you would draw a number of parallel field lines equally spaced and perpendicular to the face.

No, I understand this. I was just supposing the situation where we had a point charge, instead of the charge distribution in the problem--whatever that may be. So, if there was actually a point charge in it, why isn't it true that at least one electric field line is perpendicular to each face?

 

[TSny]

In that case, you're right. Each face would have one electric field line from the point charge that would be perpendicular to the face.

 

[Bashyboy]

Wow, this seems too incredible: me, correct for a change. Thank you very much, TSny.