Electric Potential of a Bent Bar?

[cat_facts]

Homework Statement

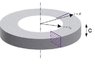
There is a bent bar with inner radius A and outer radius B and thickness C. Bar is bent from the x-axis to the y-axis in a quart circle.

1) If the bottom of the bar has potential 0 and the top has potential Vo, find Resistivity.
2) If the inner circle had potential 0 and the outer circle had potential Vo, find the Resistivity.
3) If one end has potential 0 and the other has potential Vo, find Resistivity.

Homework Equations

Ohm's Law, J = σE

The Attempt at a Solution

I attempted to find the volume of the bar, which I found to be (b^2 - a^2)*c*(pi/8). I think I now need to find an electric field, but would like a bump in a correct direction.

 

[TSny]

Hello.

Are you sure that you are asked to find the resistivity rather than the overall resistance?

Does the bar have a square cross section?

Why do you think you need to find the volume of the bar? Do you recall what geometrical quantities determine the resistance of a section of material?

 

[Dick]

Hello.

Are you sure that you are asked to find the resistivity rather than the overall resistance?

Does the bar have a square cross section?

Why do you think you need to find the volume of the bar? Do you recall what geometrical quantities determine the resistance of a section of material?

That is a strange question. Even aside from the ambiguities in the description of the shape and boundary conditions and resistivity vs resistance. There are very few geometrical configurations where you can give an exact answer for the resistance of a shape with given boundary conditions. Basically you need an exact solution to Laplaces equation. So rectangle between two ends (easy), conformal transforms of that shape and other really special situations. This caught my eye because I worked on finding solutions to problems like this using finite element analysis. I suppose you could give some sort of plausible approximation by hand waving. Suppose that's what they want.

 

[TSny]

That is a strange question. Even aside from the ambiguities in the description of the shape and boundary conditions and resistivity vs resistance. There are very few geometrical configurations where you can give an exact answer for the resistance of a shape with given boundary conditions. Basically you need an exact solution to Laplaces equation. So rectangle between two ends (easy), conformal transforms of that shape and other really special situations. This caught my eye because I worked on finding solutions to problems like this using finite element analysis. I suppose you could give some sort of plausible approximation by hand waving. Suppose that's what they want.

Good point. I'm reminded of a problem in the Halliday, Resnick Walker introductory physics text. You're asked to find the resistance between ends of a truncated cone. See http://www.chegg.com/homework-help/questions-and-answers/figure-current-set-truncated-right-circular-cone-resistivity-875-m-left-radius-200-mm-righ-q1511807.

Note that they say to assume the current density is uniform across any cross section. I guess that's an assumption that would not actually be correct if you just kept the two ends at some fixed potentials. But, nevertheless, making that assumption leads to a nice exercise.

 

[Dick]

Good point. I'm reminded of a problem in the Halliday, Resnick Walker introductory physics text. You're asked to find the resistance between ends of a truncated cone. See http://www.chegg.com/homework-help/questions-and-answers/figure-current-set-truncated-right-circular-cone-resistivity-875-m-left-radius-200-mm-righ-q1511807.

Note that they say to assume the current density is uniform across any cross section. I guess that's an assumption that would not actually be correct if you just kept the two ends at some fixed potentials. But, nevertheless, making that assumption leads to a nice exercise.

That's a good example of one of the easy ones. It's basically the same as an annulus between the inside radius and the outside radius. There's an exact symmetry which let's you determine the direction current flows everywhere. If you start bending it, that symmetry breaks. In the given problem I think you could probably handle the inside-outside case that way because it's easy to find equipotential surfaces. In the others, you can't. And I should probably even rethink the inside-outside case. I have a nagging feeling I'm probably wrong.

 

[TSny]

My best guess for the geometry of the OP question is that the bent rod is a section of a square cross-section torus, as shown in the picture but consisting of just a quarter of the full torus (between the two purple cross sections). At least that agrees within a factor of 2 with the OP's volume expression. Radius A and B of OP correspond to r₀ and R in the picture.

If so, would finding R be straightforward for the following two cases?
(1) R between top and bottom
(2) R between inner radius r_o and outer radius R

but not straightforward between the two square ends because of the bending?

Apologies to cat_facts if I'm misinterpreting the geometry.

 

[Dick]

My best guess for the geometry of the OP question is that the bent rod is a section of a square cross-section torus, as shown in the picture but consisting of just a quarter of the full torus (between the two purple cross sections). At least that agrees within a factor of 2 with the OP's volume expression. Radius A and B of OP correspond to r₀ and R in the picture.

If so, would finding R be straightforward for the following two cases?
(1) R between top and bottom
(2) R between inner radius r_o and outer radius R

but not straightforward between the two square ends because of the bending?

Apologies to cat_facts if I'm misinterpreting the geometry.

From inner radius to outer radius I think you are ok. Between top and bottom you are definitely not ok. The current density (hence potential gradient) will be higher towards the inside of the loop. The current flow will try to take the shortcut to minimize energy. It won't flow symmetrically around the loop. Doesn't that fit with your 'gut feeling'?

 

[TSny]

Between top and bottom you are definitely not ok. The current density (hence potential gradient) will be higher towards the inside of the loop. The current flow will try to take the shortcut to minimize energy. It won't flow symmetrically around the loop. Doesn't that fit with your 'gut feeling'?

By "top" and "bottom" I meant the horizontal surfaces separated by the vertical distance C. My intuition for that case is that it should be straightforward.

But, for current flowing around the loop, I agree with possible difficulty there.

 

[Dick]

By "top" and "bottom" I meant the horizontal surfaces separated by the vertical distance C. My intuition for that case is that it should be straightforward.

But, for current flowing around the loop, I agree with possible difficulty there.

Yeah, I meant around the loop. Of course if all of the dimensions are small compared with the the length of the arc, then you can treat it as a 'wire' to a good approximation. That's probably what the original problem is sort of about. But I'll give you an example of the real problem. Draw three squares in the form of an L. If you apply a potential to the top of the L and to the side of the L, it would seem like somebody should know an exact answer to the resistance, yes? Last I checked they don't. There are known upper bounds and lower bounds, but no exact solution.

 

[TSny]

OK, thanks. I can imagine that current and potential distributions would get messy in the L, especially near the right angle turn. :yuck:

 

[cat_facts]

i actually do need to find the resistance, and not the resistivity. since that is just 1/σ. the geometry tsny is using is perfect, but a quarter circle instead of a full circle. isn't it just

I = (σA/L)* V

then R = L/σA?

would the strength of Vo matter to the problem? I get that it just cancels out.

 

[TSny]

i actually do need to find the resistance, and not the resistivity. since that is just 1/σ. the geometry tsny is using is perfect, but a quarter circle instead of a full circle. isn't it just

I = (σA/L)* V

then R = L/σA?

would the strength of Vo matter to the problem? I get that it just cancels out.

Yes. Good. [EDIT: Just use R = L/σA, no need to assume a value of V_o. But, you might need to break the bar into appropriate small sections or strips and apply R = L/σA to each strip and integrate. As Dick pointed out, even this might give only an approximate answer.]