- #1
Mitchtwitchita
- 190
- 0
Homework Statement
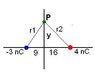
A -3.0 nC charge is on the x-axis at x = -9cm and a +4.0 nC charge is on the x-axis at x = 16 cm. At what point or points on the y-axis is the electric potential zero?
Homework Equations
V = kq/r
The Attempt at a Solution
I know the answer is +/- 12 cm but I have no clue as to how that number was achieved. Can anybody please help me out with this one?