- #1
davon806
- 148
- 1
Homework Statement
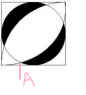
In the attached diagram,the edge of the square is a. find the area of the shaded region
Homework Equations
area of circle = πr^2 ,area of square,triangles
(Please avoid using integration/radian angle/tangent...Since this problem is found in a maths exercise suitable for a 12-year-old..)Thanks
The Attempt at a Solution
The unshaded corners of the square is easy.The "diagonal leaf" is easy as well.But I have been struggling to find the small portion(marked as A in my diagram) Looking for some insight.Thanks!
Btw,the book mentioned that it might be helpful to draw the same leaf on the left diagonal