- #1
ScienceGeek24
- 164
- 0
Homework Statement
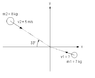
Mass m1=7kg with speed of 3 m/s collides at the origin with a mass m2= 8 kg that has a speed of 5 m/s, (at an angle of 33 degree in the 2nd qwuadrant). After the collision , mass 2 remains at rest at the origin. Find the final velocity of mass 1 (magnitude and direction).
Homework Equations
vf=m1+m2/m1-m1 time vx
vf=2m/m1+m2 vy
The Attempt at a Solution
I tried using this equation to get the right answer which is 3.59m/s by doind this (2(8kg)cos(33)/7kg+8kg time 5 m/s and i get 4.47 m/s. What I'm I doing wrong here?