Energy and Linear Momentum

[ericoromero]

Homework Statement

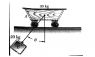
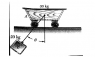
Consider the situation shown in the picture below. Cart A has a mass of 30kg and rests on a horizontal track with negligible friction. A 20kg mass (B) is suspended from a cable of length 2m from a connection point on cart A. Mass B is raised with the cable kept taught through an angle Ѳ=35° and then released.

1. In what direction is the system isolated from external forces?
2. What is the initial Linear momentum of the system?
3. Draw a diagram to show the final state of the system, and write an equation for the final momentum of the system.
4. Perform an energy analysis to determine the relationship between the given parameters and the unknown variables.
5. Find the velocity of the cart and mass(B) relative to the stationary track when the cable is vertical while mass B is swinging.
6. What is the normal force on the cart when the cable is vertical while mass B is swinging?

Homework Equations

Ei+Ef since its an isolated system. KE=.5mv^2, GPE=mgh, L(momentum)=mv
Diagram attached.

The Attempt at a Solution

I need a nudge in the right direction. I am practicing for my final exam and have had difficulty with this concept throughout the semester. Any help is very appreciated.

 

[haruspex]

Ei+Ef since its an isolated system.

You mean Ei=Ef, right? But it is not true that the cart+mass form a completely isolated system. They're not hanging about in empty space.
You need to show more attempt at answering some of these questions.

 

[ericoromero]

yeah i meant Ei=Ef, and i meant its isolated about the x-axis. As for the y-axis there is gravity

 

[ericoromero]

So far I have this. Am I on the right track?

 

[haruspex]

Am I on the right track?

Yes, those two answers are correct.

3. Draw a diagram to show the final state of the system, and write an equation for the final momentum of the system.

If the friction is to be ignored then this question doesn't make sense. There is no final state. However, you can say something about the momentum of the system at any arbitrary later time.

4. Perform an energy analysis to determine the relationship between the given parameters and the unknown variables.

You need to make some reasonable guess of what is meant here by the unknown variables.

5. Find the velocity of the cart and mass(B) relative to the stationary track when the cable is vertical while mass B is swinging.

Try this one. What physical laws do you think may be relevant?

 

[ericoromero]

I finished the rest. I just went with my gut and would really appreciate someone reviewing my work. Thank you again.

 

[ericoromero]

The pictures were accidentally put in reverse order, so the bottom right corner is questions #3 and the top left picture is questions #6

 

[haruspex]

The pictures were accidentally put in reverse order, so the bottom right corner is questions #3 and the top left picture is questions #6

Please don't post images of handwritten working. It makes more work for those trying to give you answers. Pls post as typed text in the post, preferably using latex.
In Q4, eqn 3, why the 'i' suffixes?
In your expression for T, you've forgotten something.
Two of your images came out sideways. I have not read them.

 

[ericoromero]

I'm sorry about that. I'm not familiar with latex yet. I was confused about initial and final values of L. Does T=m_b*V_b²/2 + m_bg?

 

[haruspex]

Does T=m_b*V_b²/2 + m_bg?

Yes, but it makes things clearer if you keep all data items in symbolic form, only plugging in numbers at the end. E.g. it would be better to write T=m_b*V_b²/L + m_bg (having defined L).

 

[ericoromero]

I see. I am also having a bit of trouble with isolating V_b and V_A. Would the GPE=KE+L?

 

[haruspex]

Sorry, I've confused things by using L for length of rope when you were already using L for momentum. Let me change that to T=mb*Vb2/D + mbg.

Would the GPE=KE+L?

Where L is momentum? No, you can't mix energy and momentum like that. What does the conservation law say?

 

[ericoromero]

My first thought was: Initially there is only GPE, b/c initial velocity is 0. Once the object is in motion, (the reference point in the y direction, being where theta=0, when h_b=2) that there would be two forms of energy, both GPE and KE. I thought GPE_i=KE + GPE, but I couldn't figure out how to isolate V_A or V_b, so i eliminated that option. I was then confused as threw in momentum.

 

[haruspex]

I thought GPE_i=KE + GPE

Stick with that.

I couldn't figure out how to isolate VA or Vb

There are two facts you need to bring in:
- conservation of horizontal momentum (or, equivalently here, of horizontal mass centre)
- constancy of length of rope
When the rope is at angle $\phi$ to the vertical, where are the cart and suspended mass along the x co-ordinate from the common mass centre?

 

[ericoromero]

I am still confused. I don't know how to answer that question.

 

[ericoromero]

Can I view the masses as one so that instead of having M*V+M*V=L, I have V(M+M)=L? Don't mind the lack of subscripts.

 

[haruspex]

Can I view the masses as one so that instead of having M*V+M*V=L, I have V(M+M)=L? Don't mind the lack of subscripts.

No, they're moving at different horizontal speeds.

I don't know how to answer that question.

When the cart is distance x to the right of the common mass centre, how far is the suspended mass to the left? Knowing the length of the rope, how do those distances relate to the angle of the rope?

 

[ericoromero]

The angle would be equal to the arcsin of 2(length of the rope)/x(the distance of the cart from the common mass centre.

 

[haruspex]

The angle would be equal to the arcsin of 2(length of the rope)/x(the distance of the cart from the common mass centre.

No, a couple of things wrong there. If the cart is distance x to the right of the c.o.m., how far is the mass to the left? What total distance is that?

 

[ericoromero]

The mass would be 2(1-cos(theta)) away.?
since M_B*V_B+M_A*V_A=0, I manipulated that equation to be, 2(V_B-V_A)=3V_A. I made V_A negative b/c its moving away from the origin, then I input the masses. And since the mass is attached to the cart, I used V_B-V_A, instead of only V_B

 

[haruspex]

The mass would be 2(1-cos(theta)) away.?

No.

since M_B*V_B+M_A*V_A=0, I manipulated that equation to be, 2(V_B-V_A)=3V_A.

Try that again. On second thoughts, don't - keep everything symbolic as long as possible. Don't substitute in the mass values until the end.

I made V_A negative b/c its moving away from the origin, then I input the masses.

Best to keep one direction as positive for all displacements, speeds, accelerations. Less confusing in the long run.

And since the mass is attached to the cart, I used V_B-V_A, instead of only V_B

Again, less confusing if we work with absolute speeds, not relative speeds.

 

[ericoromero]

I am really lost at this point, especially about the distances from the COM. Do I have to find the COM? I will have to look over some lecture notes. I feel stuck. Thank you for all your help.