- #1
msw1
- 5
- 2
- Homework Statement
- (Figure 1) shows two processes, A and B, for moving 3.45 × 10^22 particles of a monatomic ideal gas from state i to state f. Which process requires a smaller magnitude of the energy Q transferred thermally to the gas?
- Relevant Equations
- $$\Delta E=W+Q$$
$$PV=Nk_BT$$
$$Q=\tfrac{d}{2}Nk_BT \text{ (isochoric process)}$$
$$Q=NC_p\Delta T \text{ (isobaric process) }$$
Here is the figure:
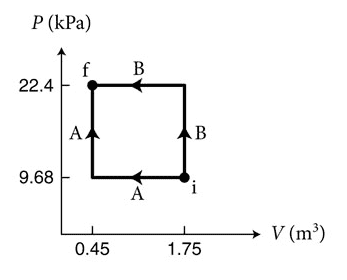
The answer is $$Q_A<Q_B$$ which I can show by calculation using the above equations. What's confusing to me is I thought that the change in internal energy was a state function. Which would mean since the initial and final points are the same, $$\Delta E_A=\Delta E_B$$ or by the 1st law of thermodynamics $$W_A+Q_A=W_B+Q_B$$ Since W is the area under the curve (and positive in this case since the gas is being compressed), $$W_A<W_B$$ So the work done on the gas in process A is less than in process B, and the energy transferred thermally to the gas in process A is less than in process B. Which, since all values are positive, seems like it contradicts the original assumption that the change in internal energy was a state function, since it seems like the change in internal energy has to be less in process A. What am I missing here?
The answer is $$Q_A<Q_B$$ which I can show by calculation using the above equations. What's confusing to me is I thought that the change in internal energy was a state function. Which would mean since the initial and final points are the same, $$\Delta E_A=\Delta E_B$$ or by the 1st law of thermodynamics $$W_A+Q_A=W_B+Q_B$$ Since W is the area under the curve (and positive in this case since the gas is being compressed), $$W_A<W_B$$ So the work done on the gas in process A is less than in process B, and the energy transferred thermally to the gas in process A is less than in process B. Which, since all values are positive, seems like it contradicts the original assumption that the change in internal energy was a state function, since it seems like the change in internal energy has to be less in process A. What am I missing here?