Discussion Overview
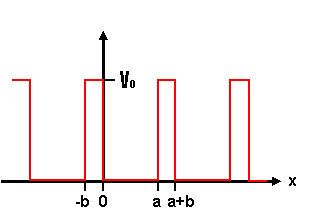
The discussion centers around the Kronig-Penney model, specifically focusing on the solutions to the time-independent Schrödinger equation within and outside a periodic potential. Participants explore the mathematical formulation of the wavefunctions in different potential regions and the implications for energy band structures.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Exploratory
Main Points Raised
- One participant questions why the solution in the region of -b < x < 0 does not involve complex exponentials, unlike the region of 0 < x < a.
- Another participant explains that in the region -b < x < 0, the wavefunction must decay, which requires the argument of the exponential to be real, leading to a specific form of the solution.
- There is a discussion about the second-order ordinary differential equation (ODE) in both regions, with participants confirming that both regions indeed represent second-order ODEs.
- One participant describes the solutions in the region with V=0 as traveling waves, indicating the nature of the wavefunctions in that area.
- A later reply expresses gratitude for clarifications and acknowledges previous conceptual errors regarding the wave equation.
- Another participant seeks guidance on reproducing band structure diagrams and outlines the wavefunctions for different potential regions, along with boundary conditions that must be satisfied.
- The same participant raises a question about defining allowed and forbidden energy values based on the determinant derived from the boundary conditions.
Areas of Agreement / Disagreement
Participants appear to agree on the mathematical formulation of the wavefunctions in different regions, but there is no consensus on how to define the allowed and forbidden energy values, as this remains an open question in the discussion.
Contextual Notes
Participants reference boundary conditions and the application of Bloch's theorem, indicating that the discussion involves complex mathematical relationships and assumptions that may not be fully resolved.
Who May Find This Useful
This discussion may be useful for students and researchers interested in quantum mechanics, particularly those studying solid-state physics and the mathematical modeling of energy bands in periodic potentials.