Explore How Physicists Prove Energy Conservation

[Biker]

I am not defying any law here just asking.

Energy conservation.
I was really wondering, How physicists arrived to this law?
I was fine with it, solving problems and stuff. But sometimes things click in my mind.
Perhaps confusionleads to a better understanding...

We can prove mathematically that energy is conserved for example a falling object or for some easy problems.
But how about complex mechanics? Can we prove it mathematically too? or should we just generalize it? Have we arrived to this law by experimenting? for example this

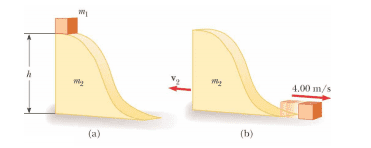
I can keep track of the forces and say that momentum is conserved (Newton third law, However I am also confused why the wedge wouldn't move at an angle because there is some parts where the force acting on it is has a Y component. Perhaps the ground is pushing upward? but that wouldn't be conserved for the system of block and wedge.. ??)Anyway, I can use the same way above to show the energy is conserved, Can't I ?

Also, I have read on some articles. That our energy conservation principle doesn't happen all the time in the universe and there is in some condition some energy lost. What does this mean to you (The person who is answering) as a physicist? That our laws aren't right enough to be applied universally?

I know it is a foundation of a lots of fields of science we have today, That is why I am trying to get full prospective of it.

 

[Dale]

But how about complex mechanics? Can we prove it mathematically too?

Yes, this is called the work energy theorem. Another important theorem in this regards would be Noether's theorem.

 

[BvU]

Something gives mee the feeling referring to aunt Emmy is't all that helpful for Biker .
Bottom line of her theorem is that a symmetry leads to a conserved quantity. In our case symmetry in space leads to energy conservation and symmetry in time leads to momentum conservation (*). Easy to say, hard to get your head around in reality. Took mankind quite a while.

(*) think of Energy = Force * displacement for the first, and Force = $\Delta$momentum/$\Delta$ time for the second.

So I'll throw in a few remarks on the example in post #1. Doesn't say the wedge is on a smooth horizontal surface and there is no friction between wedge and block either. So let me state that here.

there is some parts where the force acting on it is has a Y component. Perhaps the ground is pushing upward? but that wouldn't be conserved for the system of block and wedge.. ??)

well, the block pushes down, so the wedge wants to go down -- is that what you mean ? Because the wedge can not go down, the smooth surface must exercise an equal and opposite force upwards to the tune that there is no vertical component in the net force on the wedge. So yes, the ground is pushing upward (the normal force) and it this normal force is indeed not constant in time. It is not a conserved quantity. And it does no work: the displacement in the direction of the force is zero.

We can prove mathematically that energy is conserved for example a falling object or for some easy problems.
But how about complex mechanics? Can we prove it mathematically too? or should we just generalize it? Have we arrived to this law by experimenting?

Good questions. Energy conservation goes a long way. What complicates the grasp is that energy can take on so many forms. The genius of folks like Galilei, Newton, etc. (Carnot,Joule, ..) is that they could combine observations with generalization, extrapolation and out-of-the-contemporary-box thinking.

 

[wrobel]

The law of conservation of energy as well as any other laws of conservation are just the first integrals of differential equations of dynamics. It is pure mathematical thing: there is ODE and there is its first integral. Indeed in case of the Lagrange equations the main important integrals are generated by symmetries of the configuration space and time. These integrals follow from the Noether theorem. However some problems possesses first integrals that do not follow from the Noether theorem.

A smooth function $f(x)$ is a first integral to system $\dot x^k= v^k(x)$ iff $$\frac{\partial f}{\partial x^i}v^i=0$$

 

[Biker]

Something gives mee the feeling referring to aunt Emmy is't all that helpful for Biker .
Bottom line of her theorem is that a symmetry leads to a conserved quantity. In our case symmetry in space leads to energy conservation and symmetry in time leads to momentum conservation (*). Easy to say, hard to get your head around in reality. Took mankind quite a while.

(*) think of Energy = Force * displacement for the first, and Force = $\Delta$momentum/$\Delta$ time for the second.

So I'll throw in a few remarks on the example in post #1. Doesn't say the wedge is on a smooth horizontal surface and there is no friction between wedge and block either. So let me state that here.
well, the block pushes down, so the wedge wants to go down -- is that what you mean ? Because the wedge can not go down, the smooth surface must exercise an equal and opposite force upwards to the tune that there is no vertical component in the net force on the wedge. So yes, the ground is pushing upward (the normal force) and it this normal force is indeed not constant in time. It is not a conserved quantity. And it does no work: the displacement in the direction of the force is zero.
Good questions. Energy conservation goes a long way. What complicates the grasp is that energy can take on so many forms. The genius of folks like Galilei, Newton, etc. (Carnot,Joule, ..) is that they could combine observations with generalization, extrapolation and out-of-the-contemporary-box thinking.

Thanks to everyone!

and thank you so much BvU for as always great answers :D

Okay, So we say that there is a force acting that the ground is exerting to equalize the force results from the block sliding in the y direction for the wedge, the weight of the wedge and the block. So that means pretty much that there is no external force in the system and only internal forces which says if the block loses some of its energy it becomes kinetic energy for the incline. Energy conservation done!

Lets get back to the momentum conservation again :/, If you consider a simple wedge and at the end of it smooth transition
The force that will be acting on it the whole time is $mg sin θ$ where theta changes at the bottom.
And the wedge will only have $mg sin θ cos θ$ So clearly until the edge of the wedge (before the smooth transition part) momentum is not conserved. So the smooth transition has the effect of keeping momentum conserved?And let's finish the last question (It was in the original post):
Also, I have read on some articles. That our energy conservation principle doesn't happen all the time in the universe and there is in some condition some energy lost. What does this mean to you (The person who is answering) as a physicist? That our laws aren't right enough to be applied universally?

 

[Nugatory]

And the wedge will only have $mg sin θ cos θ$ So clearly until the edge of the wedge (before the smooth transition part) momentum is not conserved.

Momentum is conserved even while the block is sliding down the incline. It doesn't look that way because the block is gaining speed in one direction while the wedge and the entire planet Earth to which it is attached appear to be standing still - but in fact the Earth is moving ever so slightly in the opposite direction under the influence of the gravitational force between the block and the Earth and the force of the block pushing on the wedge pushing on the earth. It's a good exercise to calculate the change in speed of the Earth needed to conserve momentum throughout the entire slide - you'll see why it's easier just to treat the Earth as motionless throughout.

 

[BvU]

The force that will be acting on it the whole time is $mg\sin\theta$ where theta changes at the bottom.
And the wedge will only have $mg \sin \theta \cos \theta$ So clearly until the edge of the wedge (before the smooth transition part) momentum is not conserved.

Sort of, yes. Horizontally things are OK (block gets $mg \sin \theta \cos \theta$ too -- the $mg\sin\theta$ is along the incline). But vertically the block gains speed and loses it in the instant it hits the floor. Bottom line for this exercise is that the center of mass has lost potential energy (grravity has done work m₁gh) and that energy has been converted into kinetic energy. How that kinetic energy is distributed over the two parts follows from (horizontal) momentum conservation.

Also, I have read on some articles. That our energy conservation principle doesn't happen all the time in the universe and there is in some condition some energy lost. What does this mean to you (The person who is answering) as a physicist?

Not much until I know more about the context. In relativity you can trade mass for energy, but that's about it, methinks.

 

[Nugatory]

And let's finish the last question (It was in the original post):
Also, I have read on some articles. That our energy conservation principle doesn't happen all the time in the universe and there is in some condition some energy lost. What does this mean to you (The person who is answering) as a physicist? That our laws aren't right enough to be applied universally?

No, energy conservation always works. You just have to be very careful about how you phrase it to get something that applies universally. Something along these lines will work:

In any small volume of space, the net change in the total amount of energy in that volume over time will equal the amount of energy that flows into that volume over the same time, minus the amount that flows out. You have to count mass as a form of energy using $E=mc^2$.

(If this doesn't make sense, try thinking about pouring water into a leaky bucket - net change in the amount of water in the bucket is the amount we pour in, minus what leaks out.)

 

[Biker]

No, energy conservation always works. You just have to be very careful about how you phrase it to get something that applies universally. Something along these lines will work:

In any small volume of space, the net change in the total amount of energy in that volume over time will equal the amount of energy that flows into that volume over the same time, minus the amount that flows out. You have to count mass as a form of energy using $E=mc^2$.

(If this doesn't make sense, try thinking about pouring water into a leaky bucket - net change in the amount of water in the bucket is the amount we pour in, minus what leaks out.)

Thank you both, I am going to read your notes and post about it tomorrow.

The condition where energy dissipates was when light gets stretched out by space expansion

 

[DrClaude]

In our case symmetry in space leads to energy conservation and symmetry in time leads to momentum conservation

That's actually the other way around

 

[Nugatory]

The condition where energy dissipates was when light gets stretched out by space expansion

That's one of several situations (all most relevant at cosmological scales) that require the very careful statement of energy conversation that I posted.

 

[BvU]

That's actually the other way around

Oops, mixed up . Thanks, Claude. 'The (*) Think of' is far too simplistic. Better read the full story, e.g. here -- unless someone knows a link for a more accessible version ?

 

[Leesa Johnson]

I think that is not true that energy is lost in the work energy theorem. When the work is done there will be a cause that there is a change in the kinetic energy. If we found deeply on the object about the impact of the work then we will be able in find out the destination of the energy. If you could provide some example of energy lost then I will give the answer more effectively.

 

[Biker]

Momentum is conserved even while the block is sliding down the incline. It doesn't look that way because the block is gaining speed in one direction while the wedge and the entire planet Earth to which it is attached appear to be standing still - but in fact the Earth is moving ever so slightly in the opposite direction under the influence of the gravitational force between the block and the Earth and the force of the block pushing on the wedge pushing on the earth. It's a good exercise to calculate the change in speed of the Earth needed to conserve momentum throughout the entire slide - you'll see why it's easier just to treat the Earth as motionless throughout.

So I was really thinking about this ( Kinda of busy with school's final) in order for momentum to be conserved the earth, probably the wedge too and possibly the block should be moving upward.

Lets first take the moment where everything was stationary. Earth is being pulled by the to blocks with mg forces in their direction and the blocks are being pulled by earth. However the downward force on the wedge is $m_{wedge}~ g + m_{block}~g (cos θ)^2$
Now in order to start working on it because I have no idea where to start from. I have to find the common acceleration that is upward for all of them so they can be relative to each other stationary? Probably messing a lot of concept but bear with me professor :/

and all that momentum upward with the momentum of the wedge should cancel out the momentum of the block?

Sort of, yes. Horizontally things are OK (block gets $mg \sin \theta \cos \theta$ too -- the $mg\sin\theta$ is along the incline). But vertically the block gains speed and loses it in the instant it hits the floor. Bottom line for this exercise is that the center of mass has lost potential energy (grravity has done work m₁gh) and that energy has been converted into kinetic energy. How that kinetic energy is distributed over the two parts follows from (horizontal) momentum conservation.
Not much until I know more about the context. In relativity you can trade mass for energy, but that's about it, methinks.

So hmm we are talking here about the system of the block and the wedge only right..

Yea, before you posted, I posted a similar answer to this. So yes momentum is conserved when it hits the ground.
But if you apply energy conservation here, It shouldn't work should it? ( The system of the block and wedge) because the system lost energy by losing the vertical velocity for both the wedge and the block. So in order do apply energy conservation should I take the system of

 

[Nugatory]

So I was really thinking about this ( Kinda of busy with school's final) in order for momentum to be conserved the earth, probably the wedge too and possibly the block should be moving upward.

Yep. Gravity is pulling the block and the Earth toward one another, which means that the Earth is pulled upwards and the block downwards relative to the initial position of the earth. The wedge is forcing the block to the right, which means that the Earth is being forced to the left.

Net, the block moves down and to the right while the Earth moves up to the left. At the bottom of the ramp the block and the Earth collide, their equal and opposite momenta cancel, and they both end up at rest again.

 

[Biker]

Yep. Gravity is pulling the block and the Earth toward one another, which means that the Earth is pulled upwards and the block downwards relative to the initial position of the earth. The wedge is forcing the block to the right, which means that the Earth is being forced to the left.

Net, the block moves down and to the right while the Earth moves up to the left. At the bottom of the ramp the block and the Earth collide, their equal and opposite momenta cancel, and they both end up at rest again.

"in fact the Earth is moving ever so slightly in the opposite direction under the influence of the gravitational force between the block and the earth"
"which means that the Earth is being forced to the left."
Is there is a need for the Earth to move to the left? The wedge's momentum which is to the left should just perfectly cancel out the momentum of the block to the right
and I am left with the momentum of the block being downward so the Earth should just move upward (with the block and the wedge)..?

I was also trying to see the individual body analysis which perhaps would give me a better view of this.
On earth, There should be $(M + m) g$ upward and $N_{between~earth~and~wedge}$ downward and the net force should be upward
On wedge, There should be $Mg + mg (cos θ)^2 + N_{between~block~ and~wedge}$downward and $N_{between~earth~and~wedge}$
on the block, $N_{between~block~and~wedge}$ upward with the forces that it already has..
Where $(M + m) g > N_{between~earth~and~wedge} > Mg + mg (cos θ)^2 + N_{between~block~and ~wedge}$
and we relate all of them by a common acceleration. Or we could just find the net force on the vertical axes ( caused by gravity) and treat it as a one block $(M_{earth} + m_{wedge} + m_{block} ) a_y$

I would be actually surprised if this is right.

Thanks again.

 

[Nugatory]

Is there is a need for the Earth to move to the left? The wedge's momentum which is to the left should just perfectly cancel out the momentum of the block to the right

That depends on whether the wedge is solidly fastened to Earth or not. I was assuming that it was, but if the wedge is free to slide frictionlessly on the surface of the Earth then you're right - the wedge slides to the left while the Earth does not.

 

[BvU]

That depends on whether the wedge is solidly fastened to Earth or not

The $v_2$ in the picture suggests it isn't solidly fastened

 

[Biker]

As you didnt say anything about the ways I suggested above it is correct then.

So I am going use both ways by substituting random values and will see how it goes. The difference between the two results should be really low because that might be a reason why neglect the moving earth.

Thanks!

 

[Jeroen537]

Can I put in my 2₵ worth?

The way I understand Biker (of course it's for him to say) is the following: how did physicists arrive the conclusion that energy is always conserved?

If I am right here, most of the answers address a very different question, namely: How can it be proven that energy is always conserved?

The first question is about our knowledge of nature and how it came about, the second is about mathematical proof. Needless to point out here that mathematical proof can never definitely determine the truth of a statement about nature, since all depends on the truth of the assumptions one starts with (and also on the validity of our logic as applied to nature), and these are always potentially subject to falsification through experiment.

The latter question (about provability) has been convincingly addressed in the answers above. The first has not.

A quick Internet search revealed much literature on it. See e.g. the references in the Wikipedia article about energy conservation (https://en.wikipedia.org/wiki/Conservation_of_energy#History_of_ideas).

Hope this sheds some additional light on the question.PS At the risk of pointing out the obvious: physicists do not know for a fact whether energy is always conserved. They just have never found an exception, if they were careful to take account of all forms that they think energy can take. Barring evidence to the contrary, they assume it's true.

If needed, I have an authority to back me up here:

There is a fact, or if you wish, a law, governing all natural phenomena that are known to date. There is no known exception to this law—it is exact so far as we know. The law is called the conservation of energy. It states that there is a certain quantity, which we call energy, that does not change in the manifold changes which nature undergoes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number and when we finish watching nature go through her tricks and calculate the number again, it is the same. [My emphasis J.]​

(The Feynman Lectures on Physics, Vol. I, Ch. 4)