Energy in standing waves?

[Shing]

Suppose I have a string that has completely no motion.

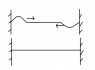
at t=0, I give it energy, two waves.

at t=t'. I see destructive interference from the two waves.

question: At t=0, the net energy must be positive, >0, then at t=t', where is the energy?
(let the waves "meet" at x=L, most of the points at x=L during destructive interference has speed zero, so K.E.=0 , and if all the energy become P.E., then what is the difference to a string without any energy at the first place?)

Thanks for reading :D

 

[foges]

Just because displacement is zero, does not mean that velocity is zero. If you take a guitar string and excite it to its first harmonic (ie. $$d=\lambda/2$$), while swinging back and forth, twice every period the string will have a displacement of zero (relative to a motionless string), but a non-zero velocity in the direction normal to the string.. In your example, when the two waves meet, the left part of the string will have a downwards velocity whilst the right part will have an upward velocity. Energy gets conserved.

Hope that helped :)

 

[Studiot]

I would be interested to learn how you think you could cause a string, stretched between two fixed points, to take up the shape you have drawn?

If you pluck it at the points show, upwards on the left and downwards on the right, the centre portion will tilt between the two peaks. Thus you will have a central node plus one at each end.

What you will not achieve is the generation of two traveling waves as shown, nor the destructive interference you describe.

Once you realize this you will see that the energy you input will be manifest a standing wave with three nodes and two anti nodes.

go well

 

[Shing]

Thanks for your answering :D

Just because displacement is zero, does not mean that velocity is zero.
Hope that helped :)

well, let x=L, where the waves meet, at x=L, its velocity must be zero, because displacement must be zero DURING destructive interference ALL THE WAY.

I would be interested to learn how you think you could cause a string,

Well, I can always cause such waves (say, using my hands) and then tie the string on the wall...

Maybe I should clarify my question:
Where does the energy go when destructive interference happens?
(given KE always >0, one of the P.E. <0, another P.E. >0, therefore, the net energy must be >0, when destructive interference happens, the region around the midpoint must have zero velocity such that during the whole destructive interference, the positions(around the midpoint of the destructive interference) remains zero.

anyway, sorry for my lousy English. English is my second language.. :O

 

[Studiot]

Well, I can always cause such waves (say, using my hands) and then tie the string on the wall...

Try again.

 

[Dale]

where the waves meet, at x=L, its velocity must be zero,
...
the region around the midpoint must have zero velocity

You have already been told that this is incorrect. The velocity is non-zero. If you disagree then please post the mathematical derivation that leads you to this conclusion.

 

[Shing]

You have already been told that this is incorrect. The velocity is non-zero. If you disagree then please post the mathematical derivation that leads you to this conclusion.

I hardly agree on the necessary of math so far here. On the other hand, isn't argument the best way to learn? I don't want any spoon-feeding.

Suppose the waves are totally equal to each other except upside down and the traveling direction, and they meet at x=L and cause destructive interference. y(x,t), -y(x,-t)

Assuming there is non-zero velocity for all x, while y(x)=0.

Then, say, after a very very very short time period after the moment we see the destructive interference, the displacement must not be zero at any point with a non-zero velocity; as

How could a destructive interference "disappear" in a very very very short time?

If my opinion is wrong, I welcome any rebukes with open arms.

 

[Shing]

Try again.

Actually, I used to think that would happen on a string (not fixed) with one hand as well,
but I think if I pull the string fast enough then I will see the wave on the string?

So wouldn't it happen on fixed string as well? If I pluck it very very fast, would I see two traveling waves instead of standing waves?

 

[Shing]

Actually, I used to think that would happen on a string (not fixed) with one hand as well,
but I think if I pull the string fast enough then I will see the wave on the string?

So wouldn't it happen on fixed string as well? If I pluck it very very fast, would I see two traveling waves instead of standing waves?

Okay! I see, I was wrong. It always a standing waves. Thanks for correction!
(How about I pluck it at a speed closed to the speed of light?)

 

[Studiot]

Hello Shing,

Now that you are thinking about the issue, have you ever made a string telephone from two empty cans and a length of string?

Pierce the bottom of each can.
Tie a knot at one end of a length of string and thread it through the hole in the bottom of one can so the knot pulls agains the bottom of the can.
Then thread the other end through the other can tie another knot.

If you and a friend pull the string tight between the cans, each holding one end. One person can talk into one can and the other can hear what is said in the second can.

You are transmitting waves along the stretched string.

These are longitudinal waves.

This is the only way to transmit waves along a stretched string.

The waves you drew were trnasverse waves.

 

[AlephZero]

These are longitudinal waves.

This is the only way to transmit waves along a stretched string.

The waves you drew were trnasverse waves.

Sorry, but it doesn't matter how many times you repeat that statement, it is just WRONG. See any textbook on dymamics, or mathematical physics, that gives the general solution of the 1-dimensional wave equation.

The OP's diagram is perfectly reasonable picture of the general idea of two "equal and opposite" transverse traveling waves moving along a string, and it is quite easy to make a real string behave like that.

Take an arbitrary wave whose shape is given by a function F(x).
The d'Alembert solution of the wave equation says this shape can travel in either direction along the string with a fixed velocity c.
So if the string has length L and you started two equal and opposite traveling waves from either end, the displacement of the string is given by

u(x,t) = F(x - ct) - F(x - L + ct)

When the waves "meet in the middle" at t = L/2c, you have
u(x,L/2c) = F(x - L/2) - F(x - L/2) = 0
which means there is destructive interference and the displacements are zero everywhere.

But the velocity is given by
u'(x,t) = -cF'(x - ct) - cF'(x - L + ct)
and when t = L/2c that is equal to
u'(x,L/2c) = -2cF'(x - L/2)
which is NOT zero everywhere, since F and therefore F' can be any shape of wave traveling along the string.

Note the "mathematical" reason for this is the sign change between the displacements and the velocities, caused by the fact that the waves are traveling in opposite directions.

 

[Studiot]

Aleph Zero,

It is a physical impossibility to pluck a horizontally stretched string once, let alone twice and leave a section horizontal.

Further the instant your string deviates from the horizontal its length must increase so its mass per unit length must also decrease, since its mass remains constant.

That is a prima facie definition of a rarefaction - which is inherent in a longitudinal wave. No such rarefaction occurs in a transverse wave.

Finally the wave equation applies equally well to longitudinal waves so obscuring the physics with some elementary maths does not alter matters.

 

[Studiot]

Let us consider the maths a moment.

A string, horizontally stretched between two fixed points A and B introduces two boundary conditions

u(x,t)_A = u(x,t)_B = 0, for all t.

Nowhere in a transverse traveling wave complying with D'Alemberts solution can such points exist.
They can, however exist in a transverse standing wave.

Which is what I said earlier.

D'Alemberts analysis refers to an infinite elastic medium as does your analysis. The minute you introduce boundary conditions, things change.

 

[marmeduke]

I have been breifly thinking about this problem and would like to give my ideas about it for some feedback.
is the reason that this diagram was false because though one could pluck the string in two places at once like shown on the diagram it will not act as a wave until it is throughout the whole string. so first the ends of both wwaves nearest the middle will rise due to a force from the rest of the raised string, so the wave gets longer until it meets destructive interference on the other side from the other wave, so the one end will rise without the other end falling? this will decrease amplitude and increase wave length. i hope I've made what I am trying to say clear enough. Also alphezero what is x in your maths? thanks

 

[Studiot]

x is the horizontal axis,

t is time

u(x,t) is the vertical displacement as a function of horizontal distance (x) and time - the y-axis if you like.

 

[Born2bwire]

Aleph Zero,

It is a physical impossibility to pluck a horizontally stretched string once, let alone twice and leave a section horizontal.

Further the instant your string deviates from the horizontal its length must increase so its mass per unit length must also decrease, since its mass remains constant.

That is a prima facie definition of a rarefaction - which is inherent in a longitudinal wave. No such rarefaction occurs in a transverse wave.

Finally the wave equation applies equally well to longitudinal waves so obscuring the physics with some elementary maths does not alter matters.

I don't see anything obviously inordinate about his setup. You can drive one of the ends of the string to create discreate transverse wave pulses. You fix the other end of the string and simply drive the opposite end so that when the first pulse has reflected you send your second pulse.

EDIT: Taking a second look there are some minor quibbles. Obviously the string will not be perfectly flat between the pulses. When we drive the end it will pull and displace the entire string. But I think such objections can be ignored since they are immaterial to the essence of the original question.

 

[Studiot]

I don't see anything obviously inordinate about his setup...
EDIT: Taking a second look there are some minor quibbles. Obviously the string will not be perfectly flat between the pulses. When we drive the end it will pull and displace the entire string. But I think such objections can be ignored since they are immaterial to the essence of the original question.

I think most thought the original sketch OK on first viewing. I certainly did.

However the string is clearly shown stretched between two walls. Do you mean jiggle the whole system, walls and all, up and down?

I agree that if A and B are not fixed points then you can snake the ends of a string up and down and send traveling pulses along it for some distance if it is slack enough. How far the pulses will get will also depend upon the characteristics of the string.

If you do not fix A and B how do you induce and maintain tension in the string?

If you fix at one point, say A, pull out at B to obtain tension and jiggle up and down, you will have a time independent node at A and an antinode at B, by definition a standing wave.

 

[Dale]

I hardly agree on the necessary of math so far here. On the other hand, isn't argument the best way to learn?

No, working problems is the best way to learn physics. It is far more effective than argument. If you cannot be bothered to do the work than at least don't ignorantly contradict people who have bothered to do it.

Did you at least read and understandunderstand the math presented by AlephZero:

When the waves "meet in the middle" at t = L/2c, you have
u(x,L/2c) = F(x - L/2) - F(x - L/2) = 0
which means there is destructive interference and the displacements are zero everywhere.

But the velocity is given by
u'(x,t) = -cF'(x - ct) - cF'(x - L + ct)
and when t = L/2c that is equal to
u'(x,L/2c) = -2cF'(x - L/2)
which is NOT zero everywhere, since F and therefore F' can be any shape of wave traveling along the string.

 

[Shing]

No, working problems is the best way to learn physics. It is far more effective than argument. If you cannot be bothered to do the work than at least don't ignorantly contradict people who have bothered to do it.

Did you at least read and understandunderstand the math presented by AlephZero:

It turns out that both are effective ways to learn.
But to me, it is boring to look at the Math without actually knowing its physical meaning (and to me, the best way to sense the physical meaning is by argument) On the other hand, just take a look on Newton's notebook, I can assure you that arguments are far more than Math. I do agree that both are important, but I am a bigger fan of argument than math

Yes, I understand what AlephZero wrote. My confusion is caused by my incomplete physics image of destructive interference, and it was argument and computer program that taught me what the system behaves when destructive interference. (the superposition of waves are NOT linear when it comes to destructive interference)

Anyway, thank you for your rebuke, I will work hard on my Math.

 

[Shing]

Hello Shing,

Now that you are thinking about the issue, have you ever made a string telephone from two empty cans and a length of string?

Pierce the bottom of each can.
Tie a knot at one end of a length of string and thread it through the hole in the bottom of one can so the knot pulls agains the bottom of the can.
Then thread the other end through the other can tie another knot.

If you and a friend pull the string tight between the cans, each holding one end. One person can talk into one can and the other can hear what is said in the second can.

You are transmitting waves along the stretched string.

These are longitudinal waves.

This is the only way to transmit waves along a stretched string.

The waves you drew were trnasverse waves.

Thank you so much.

May I ask one more question?

I would like to know how I know that if transverse waves and longitudinal waves wouldn't happen at the same system? (I mean if energy would be translated in both means?)

 

[Shing]

u(x,t) = F(x - ct) - F(x - L + ct)

When the waves "meet in the middle" at t = L/2c, you have
u(x,L/2c) = F(x - L/2) - F(x - L/2) = 0
which means there is destructive interference and the displacements are zero everywhere.

But the velocity is given by
u'(x,t) = -cF'(x - ct) - cF'(x - L + ct)
and when t = L/2c that is equal to
u'(x,L/2c) = -2cF'(x - L/2)
which is NOT zero everywhere, since F and therefore F' can be any shape of wave traveling along the string.

Thank you so much for the Math :D
In fact, we were taught that without a solid background of math in the class,
so I will work on the math in this winter break :D

 

[Studiot]

I would like to know how I know that if transverse waves and longitudinal waves wouldn't happen at the same system? (I mean if energy would be translated in both means?)

Yes indeed this happens, ask any geologist/geophysicist.

Waves in the Earth generated by earthquakes and other powerful events travel by both modes.

The transverse waves are known as S or shear waves
The longitudinal waves are known as P or pressure waves.
The P waves travel faster.
These waves travel through both the crust and some of the lower layers.

It is known that liquids can support pressure but cannot support shear, and it is observed that the P waves travel right through the Earth's core to the other side, but the S waves do not.
This is supporting evidence for the molten core theory.

Please note that this is the simplified theory, reality is more complicated, before others leap in with (minor) objections.

go well