- #1
interference
- 7
- 0
Hi everyone. This isn't a homework question; just something I was thinking about and would like some advice on how I should tackle it.
How can I approximate the Kinetic Energy Lost of a Steel Sphere when it collides with a soft sheet of material.
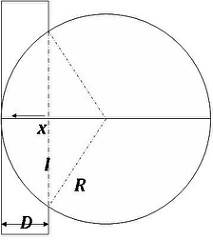
A solid steel sphere of radius R impacts a homogeneous material (e.g clay) of depth D at a velocity v. I want to find the energy imparted to the material when one side of the ball just touches the other side of the material. In other words, I can also find the final velocity of the ball and calculate the energy lost to the material.
I first write:
[tex]l=\sqrt{R^2-\left(R-x\right)^2}[/tex]
where x is the depth the ball has penetrated
and note that l refers to half of the line indicated in the diagram.
[tex]dl=\frac{l-x}{\sqrt{R^2-\left(R-x\right)^2}}dx[/tex]
I assume the steel ball and soft material have uniform density and Young's Modulus.
Where,
[tex]F=\frac{E A \Delta L}{L}[/tex]
I consider the force acted by the material with Young's Modulus E on the sphere as it burrows through facing increasing surface area of the material, given by [tex]\pil^2[/tex], where l depends on x. Then I integrate over the thickness of the material, D.
Using Hooke's Law, I write
[tex]dF=\frac{ExdA}{D}=\frac{Ex\pi\left(dl\right)^2}{D}[/tex]
Which equates the force with respect to x the amount the ball has traveled into the material. Then I integrate it from 0 to D with respect to x, and hence find the work done by the material. Is this a sound approach or did I get something really wrong?
Thanks.
Homework Statement
How can I approximate the Kinetic Energy Lost of a Steel Sphere when it collides with a soft sheet of material.
A solid steel sphere of radius R impacts a homogeneous material (e.g clay) of depth D at a velocity v. I want to find the energy imparted to the material when one side of the ball just touches the other side of the material. In other words, I can also find the final velocity of the ball and calculate the energy lost to the material.
Homework Equations
I first write:
[tex]l=\sqrt{R^2-\left(R-x\right)^2}[/tex]
where x is the depth the ball has penetrated
and note that l refers to half of the line indicated in the diagram.
[tex]dl=\frac{l-x}{\sqrt{R^2-\left(R-x\right)^2}}dx[/tex]
I assume the steel ball and soft material have uniform density and Young's Modulus.
Where,
[tex]F=\frac{E A \Delta L}{L}[/tex]
The Attempt at a Solution
I consider the force acted by the material with Young's Modulus E on the sphere as it burrows through facing increasing surface area of the material, given by [tex]\pil^2[/tex], where l depends on x. Then I integrate over the thickness of the material, D.
Using Hooke's Law, I write
[tex]dF=\frac{ExdA}{D}=\frac{Ex\pi\left(dl\right)^2}{D}[/tex]
Which equates the force with respect to x the amount the ball has traveled into the material. Then I integrate it from 0 to D with respect to x, and hence find the work done by the material. Is this a sound approach or did I get something really wrong?
Thanks.