- #1
CGandC
- 326
- 34
Let's say I have a system whose time evolution looks something like this:
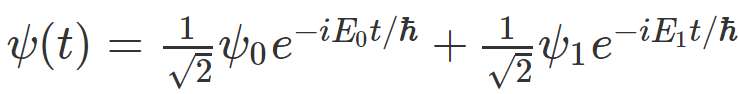
This equation tells me that if I measure energy on it, I will get either energy reading ## E_0 ## or energy reading ## E_1 ## , when I do that, the system will "collapse" into one of the energy eigenstates, ## \psi_0 ## or ## \psi_1 ## .
For example, if I have measured energy and have gotten ##E_1## , then , my system would be described by the wavefunction
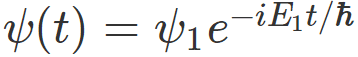
Now the question is:
If I refer to the last example , then, since I made energy measurement and have gotten ##E_1## in the measurement , then, how come is this even possible? isn't there uncertainty in every measurement? ( so that by measuring the energy , there's supposed to be some uncertainty in the measurement value of ##E_1## , but the value that was measured is exactly ##E_1## so this makes no sense to me because there is an infinite precision in the measurement )
In addition ,since now the wave function is collapsed to eigenstate corresponding to ##E_1## , then, each time I make energy measurement I will get only ##E_1## , this makes no sense to me, because isn't there uncertainty in the measurement? ( What I'm thinking is: when I make a measurement on the collapsed wave function , I will actually measure some other energy value which is close to ##E_1## but not exactly ##E_1 ## [ because of the uncertainty principle , and because each measurement of a physical paramter is actually an average value of that specific measurement ] )
This equation tells me that if I measure energy on it, I will get either energy reading ## E_0 ## or energy reading ## E_1 ## , when I do that, the system will "collapse" into one of the energy eigenstates, ## \psi_0 ## or ## \psi_1 ## .
For example, if I have measured energy and have gotten ##E_1## , then , my system would be described by the wavefunction
Now the question is:
If I refer to the last example , then, since I made energy measurement and have gotten ##E_1## in the measurement , then, how come is this even possible? isn't there uncertainty in every measurement? ( so that by measuring the energy , there's supposed to be some uncertainty in the measurement value of ##E_1## , but the value that was measured is exactly ##E_1## so this makes no sense to me because there is an infinite precision in the measurement )
In addition ,since now the wave function is collapsed to eigenstate corresponding to ##E_1## , then, each time I make energy measurement I will get only ##E_1## , this makes no sense to me, because isn't there uncertainty in the measurement? ( What I'm thinking is: when I make a measurement on the collapsed wave function , I will actually measure some other energy value which is close to ##E_1## but not exactly ##E_1 ## [ because of the uncertainty principle , and because each measurement of a physical paramter is actually an average value of that specific measurement ] )
Attachments
Last edited by a moderator: