- #1
kitz
- 11
- 0
Hi,
I'm having a bit of trouble finding the right equation for this:
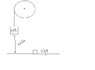
The pulley in the figure has radius 0.160 m and a moment of inertia 0.480. The rope does not slip on the pulley rim.
Use energy methods to calculate the speed of the 4.00-kg block just before it strikes the floor.
To do this, would the following formula be correct?
[tex]m_{1}gh = 1/2m_{1}v^2 + 1/2I\omega^2 + m_{2}gh[/tex]
The initial energy would just be potential, right? The 2kg block on the floor would have 0 potential energy, and 0 kinetic energy...
I'm getting an answer of 2.9352, is this correct?
I'm having a bit of trouble finding the right equation for this:
The pulley in the figure has radius 0.160 m and a moment of inertia 0.480. The rope does not slip on the pulley rim.
Use energy methods to calculate the speed of the 4.00-kg block just before it strikes the floor.
To do this, would the following formula be correct?
[tex]m_{1}gh = 1/2m_{1}v^2 + 1/2I\omega^2 + m_{2}gh[/tex]
The initial energy would just be potential, right? The 2kg block on the floor would have 0 potential energy, and 0 kinetic energy...
I'm getting an answer of 2.9352, is this correct?