- #1
burnst14
- 53
- 2
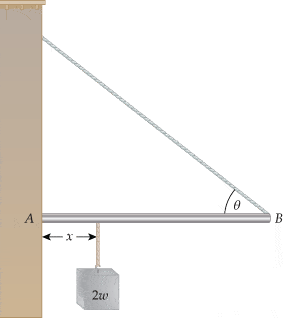
Problem Statement: As shown in the figure below, a uniform beam is supported by a cable at one end and the force of friction at the other end. The cable makes an angle of θ = 30°, the length of the beam is L = 1.50 m, the coefficient of static friction between the wall and the beam is μs = 0.420, and the weight of the beam is represented by w. Determine the minimum distance x from point A at which an additional weight 2w (twice the weight of the rod) can be hung without causing the rod to slip at point A.
Relevant Equations:
Ff = μN
Ʃτ = 0
ƩF = 0
Solution Attempt:
I'm not really sure where to start. Does Fn (normal force) come from the weight of the rod multiplied by cos(30) due to the angle of the cable holding it against the wall? And once I find Fn, I multiply that by μ, giving the upward force of friction. Then, placing the rotational axis at the end of the rod that the cable is attached to (because it's not moving, I can place the axis anywehere) and set Fn equal to the weight of the object being attached multiplied by the distance from the wall. Would that work?
Relevant Equations:
Ff = μN
Ʃτ = 0
ƩF = 0
Solution Attempt:
I'm not really sure where to start. Does Fn (normal force) come from the weight of the rod multiplied by cos(30) due to the angle of the cable holding it against the wall? And once I find Fn, I multiply that by μ, giving the upward force of friction. Then, placing the rotational axis at the end of the rod that the cable is attached to (because it's not moving, I can place the axis anywehere) and set Fn equal to the weight of the object being attached multiplied by the distance from the wall. Would that work?