- #1
Lifprasir
- 16
- 0
Homework Statement
http://puu.sh/4NWw9.PNG
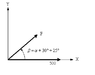
question 2.65**
Homework Equations
I've tried using the law of sine and law of cosine method with the triangle for equilibrium and I've tried the 600^2 = Fx^2 + Fy^2
The Attempt at a Solution
Here is what I did using the F^2 = Fx^2 + Fy^2
http://puu.sh/4NWDa.jpg
after that
36027 = 2*272*(500*cos 30)*cos *beta - 2*272*(500*sin 30)*cos beta
36027/(2*272*500(cos beta (cos 30-sin 30))
I get beta is 68.78 , and since beta = alpha + 25, alpha = 43.78.
However, the answer in the book is 27.4 to 222.6. I was able to get 42.6 which is just 222.6 -180, using the triangle method (i really don't know what it's called, but it's when you put draw two forces together, and you can draw the resultant force and use trig laws) but got stuck figuring out the lowest angle.
http://puu.sh/4NXg2.jpg
Here, I started off the same way as before by combining the two bottom vectors, and then I found the angle between the remaining two vectors is alpha + 55 then proceeded with a cos law, and found alpha to be 42.6 (now I am not sure if it's correct, since the answers on the back of the book specifically says 27.4 to 222.6, which is realistically impossible since the force can't go into the wall from the diagram).
Anyways, even from this method, I would not know how to solve for the lowest range of alpha, I can't set the resultant force to be 0, because there is no angle for R to be 0.
I've 2 days, a total of a good 5 hours trying to solve this, I would be blessed if someone could help me out :)
Last edited by a moderator: