- #1
DaveC426913
Gold Member
- 22,497
- 6,168
I've had discussions with laypeople (of which, I am one) about real-world manifestations of imaginary numbers. We can never seem to find a satisfactory, concise example. I know they are used in real-world calculations for things like EM wavelengths in electronics, but if you aren't into electronics, that's not much use, especially if you have to go through the math just to get it.
I finally got my head around imaginary numbers when I discovered (and correct me if I'm wrong) that any calculation that can be done with imaginary numbers, can also be done without them; it's just arbitrarily more complicated.
So I've come up with what I think is an intuitive analogue of the practical applications of imaginary numbers. I hope to explain to the lay-person why we might use imaginary numbers, even where there's no direct, real-world manifestation of them.
I draw an analogy between imaginary numbers and virtual images.
Given a diagram of a flat mirror, a point light source and an observer (pic Q), construct the point of reflection and the angle between light and observer.
This can be done by determining the X and Y distances of both points and then calculating (or constructing) the angles, but it's a bit of work.
A far simpler method is to simply reflect the image into virtual space. The incident and reflected ray become trivial to construct (pic A). A simple straight line constructs both the path and angles.
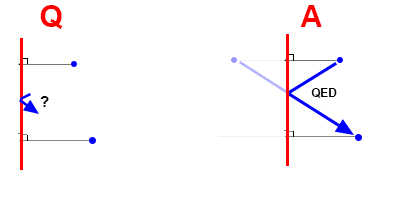
I'm hoping to demonstrate that imaginary numbers do not have to have a real-world manifestation - just like the virtual light source and light ray do not have to exist in real space - in order to be useful in a real application.
Opinions? I know it's a bit of a stretch. Virtual images are not an example of imaginary numbers, merely an analogy.
I am open to a better way of intuitive, layperson explanations.
I finally got my head around imaginary numbers when I discovered (and correct me if I'm wrong) that any calculation that can be done with imaginary numbers, can also be done without them; it's just arbitrarily more complicated.
So I've come up with what I think is an intuitive analogue of the practical applications of imaginary numbers. I hope to explain to the lay-person why we might use imaginary numbers, even where there's no direct, real-world manifestation of them.
I draw an analogy between imaginary numbers and virtual images.
Given a diagram of a flat mirror, a point light source and an observer (pic Q), construct the point of reflection and the angle between light and observer.
This can be done by determining the X and Y distances of both points and then calculating (or constructing) the angles, but it's a bit of work.
A far simpler method is to simply reflect the image into virtual space. The incident and reflected ray become trivial to construct (pic A). A simple straight line constructs both the path and angles.
I'm hoping to demonstrate that imaginary numbers do not have to have a real-world manifestation - just like the virtual light source and light ray do not have to exist in real space - in order to be useful in a real application.
Opinions? I know it's a bit of a stretch. Virtual images are not an example of imaginary numbers, merely an analogy.
I am open to a better way of intuitive, layperson explanations.
Last edited:
