Exploring Wedge Product of 0-Form and l-Form

[Maxi1995]

Hello,
we defined the wedge-product as follows

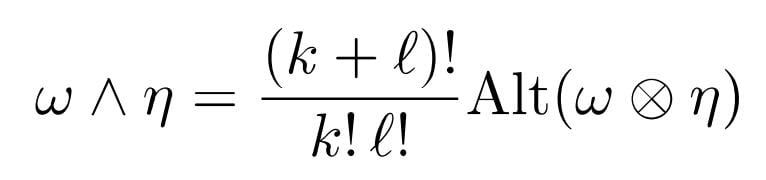
Alt is the Alternator and the argument of Alt is the Tensor poduct of one k-form and a l-form (in this order w and eta).
Suppose we have the wedge product of a 0-form (a smooth function) and a l-form , so the following may result:

$$\frac{1}{l!} \sum_{\sigma \in S_k} sgn(\sigma) f \eta(v_{\sigma(1)},...,v_{\sigma(l)}).$$

Does it hold to say that it is equal to $$f*\eta?$$

 

[Orodruin]

You really should not use $*$ here as it may be mistaken for the hodge operator.

That being said, what do you think? $f$ is clearly independent of the permutation $\sigma$ so you can move it outside the sum. It remains for you to show whether
$$
\eta(v_1, \ldots, v_\ell) = \frac{1}{\ell !} \sum_{\sigma \in S_\ell} \operatorname{sgn}(\sigma) \eta(v_{\sigma(1)},\ldots, v_{\sigma(\ell)})
$$
or not.

 

[wrobel]

In addition, * is a pseudotensor operation while $\wedge$ is a tensor one

 

[Maxi1995]

Well I weren't sure how to cope with the $$\sigma.$$ My idea was to say that we find for every permutation a counter part, that deviates only by one transposition from our permutation, so to say its form might be $$\sigma \circ \tau,$$ wehere tau is a transposition. By the alternation of the k-form, these parts should vanish. But for the transpositions in the group remain l! possibilities, so that we might get

$$\eta(v_1,...,v_k)-l!\eta(v_1,...,v_k)$$
and if that is not wrong, I don't know how to go on.

 

[fresh_42]

Well I weren't sure how to cope with the $\sigma.$

I think this is too complicated.

$\omega \wedge \eta$ is a $(k+l)-$form, so we have to define $(\omega\wedge\eta)\,(v_1,\ldots,v_{k+l})$. The formula for the alternator is
$$
Alt(\omega \wedge \eta)=\dfrac{1}{(k+l)!}\sum_{\sigma\in S_{k+l}}\operatorname{sgn}(\sigma)\,(\omega \wedge \eta)(v_{\sigma(1)},\ldots ,v_{ \sigma(k+l) } )
$$
so we have to explain
$$
\begin{align*}
(\omega\wedge\eta)\,(v_1,\ldots,v_{k+l})&=\dfrac{1}{k!\,l!}\sum_{\sigma\in S_{k+l}}\operatorname{sgn}(\sigma)(\omega \wedge \eta)\,(v_{\sigma(1)},\ldots ,v_{ \sigma(k+l) } )\\&=\sum_{\sigma\in S_{k+l}}\operatorname{sgn}(\sigma)\,\dfrac{1}{l!}\omega(v_{\sigma(1)},\ldots ,v_{ \sigma(k) }) \wedge \dfrac{1}{k!}\eta(v_{\sigma(k+1)},\ldots ,v_{ \sigma(k+l) })
\end{align*}
$$
This defines a multilinear, associative, anti-commutative and graded multiplication on $\Lambda (V) = T(V)/\langle v\otimes w-w\otimes v\rangle$.

The role of $\sigma$ is actually only the role of $\operatorname{sgn}(\sigma)$, which simply is a count of the number of mismatches in the natural order of $1,\ldots ,k+l$ which makes the entire product alternating. The factors $\dfrac{1}{l!}\; , \;\dfrac{1}{k!}$ can be considered as the amount of permutations which do not have an effect:

Say $k=2$ and $l=3$. Then for every permutation $\sigma \in S_5$ which affects the order of $(v_1,v_2)$ we have $3!$ identical versions which permute the remaining $3$ indices, which is why we cancel them via division, e.g.
$$
\omega(v_1,v_2)\stackrel{(*)}{=}\dfrac{1}{3!}\left(\sum_{\sigma=(345)}\omega(v_{\sigma(1)}+v_{\sigma(2)})+\sum_{\sigma=(354)}\omega(v_{\sigma(1)}+v_{\sigma(2)})+\sum_{\sigma=(34)}\omega(v_{\sigma(1)}+v_{\sigma(2)})+\sum_{\sigma=(35)}\omega(v_{\sigma(1)}+v_{\sigma(2)})+\sum_{\sigma=(45)}\omega(v_{\sigma(1)}+v_{\sigma(2)})+\sum_{\sigma=(1)}\omega(v_{\sigma(1)}+v_{\sigma(2)})\right)
$$
$(*)$ The sums aren't necessary here as we only sum over one term, they merely serve as a place to write the permutation $\sigma$.