- #1
namu
- 33
- 0
Homework Statement
Consider the surface defined by
F(x,y,z)=1/2(x+y)^2+(y+z)^2+(x+z)^2=9
(a) Evaluate grad(F)
My Solution:
grad(F)=(3x+y+2z, x+3y+2z, 2x+2y+4z)
(b) Find the highest and lowest points on the surface (i.e. the points where z attains a maximum or minimum).
Problem:
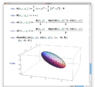
So I can solve for z=g(x,y) using the quadratic formula and get a nasty expression (see attached) and
then go about finding the extrema, but this is ugly.
If I set each component of the gradient to zero, then the only solution is (x,y,z)=(0,0,0) which is NOT an
extrema (see attached image), rather there are two extrema.
How do I do this the "easy" way?
(c) The surface is illuminated from far above by light rays that are directed parallel to the z-axis. Find the
shape of its shadow in the plane below the surface parallel to the (x,y) coordinate plane.
Problem:
So now this is projecting the surface onto the (x,y)-plane. I have no idea how to do this.
Please help.