- #1
randomafk
- 23
- 0
Homework Statement
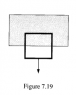
this comes from griffiths 7.46/11
A square wire loop is placed so that its top portion is in a uniform magnetic field. It is then allowed to fall under gravity. We then repeat this experiment but instead rotate the loop 45° so that it is a diamond.
Which orientation falls faster? Find the ratio of the terminal velocities.
Finally, if the loop is allowed to freely rotate, which orientations would it assume while falling?
Homework Equations
Magnetic Flux: [itex]\Phi = \int{\vec{B} \cdot d\vec{a}}[/itex]
Induced emf: [itex]\epsilon = -\frac{\partial \Phi}{\partial t}[/itex]
Induced current: [itex]I=\epsilon/R[/itex] where R= resistance
magnetic force: [itex]F_{mag}=I\int{d\vec{l} \times\vec{B}}[/itex]
The Attempt at a Solution
1) Find the flux and therefore the induced emf/current
2) Calculate the magnetic force and set it equal to mg to find the terminal velocity [itex]F=mg=F_{mag}[/itex]
I neglected the actual fomulas/ratio because it's mostly just math which isn't my difficulty.
We basically end up finding that the diamond loop falls faster until the "half way mark" at which point the square loop falls 2x faster. After this, the diamond loop falls faster again.
My difficulty is trying to figure out which orientation the loop takes on while its falling. The solutions manual says that it initially takes on the diamond orientation before switching to the square orientation at the half way mark. The manual says that this is because it attempts to "present the minimum chord at the field's edge" but I don't quite understand this explanation.
I tried to rationalize it with momentum conservation in that the loop attempts to conserve velocity since its mass is constant, so it orients itself to the square shape but I don't really know if that applies here.
Any help is appreciated! thanks.
Last edited: