Feynman Lectues Vol I Fig 11-7

[Hetware]

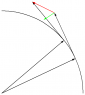
The figure 11-7 in Vol I of The Feynman Lectures appears incorrect to me. The second full paragraph explains exactly why it is incorrect. The caption should probably make it clear that the diagram represents the flawed depiction the author is warning against. Do others agree with this?

If I noticed this in the past, I didn't report the error. Unfortunately, it's still present in the New Millennium Edition.

 

[AJ Bentley]

It looks right to me - he's explicitly showing how to do it wrong then how to get it right in the next diagram - Pretty much Feynman's style.

P.S. My copy of Feynman is liberally daubed with my own notes explaining things like that.- I think he deliberately left huge margins for that purpose.

 

[DocZaius]

My conclusion is that he is using figure 11-7 for double purposes: Describing the situation, and demonstrating a wrong way to take the difference of two vectors. In addition to that, he never explicitly states that the diagram purposefully contains an example of the wrong way to do it, that is to be assumed from the text. For those reasons, I'd say Feynman is not being reasonably (a grey area!) clear here. Even a question mark after Δv in the figure would have gone a long way.

My rule for diagrams with examples of wrong way to do things is: always say so on the diagram.

 

[AJ Bentley]

My rule for diagrams with examples of wrong way to do things is: always say so on the diagram.

Feynman wrote those books in the 60's. They were a set of almost verbatim lecture notes and I've no doubt that's the diagram he drew on the blackboard.
They're a little out of context in a book - but you just have to accept that as the price you pay for his colloquial style and insight.

It's interesting that Susskind lectures the same way. Can't wait to see his book.

PS - Don't hold your breath. He won't be correcting it.

 

[DocZaius]

PS - Don't hold your breath. He won't be correcting it.

I wasn't referring to this being corrected specifically, I was just stating a rule of thumb. If I had requested for a dead man to make textbook corrections, your joke might have been more fitting ;)

 

[Hetware]

My conclusion is that he is using figure 11-7 for double purposes: Describing the situation, and demonstrating a wrong way to take the difference of two vectors. In addition to that, he never explicitly states that the diagram purposefully contains an example of the wrong way to do it, that is to be assumed from the text. For those reasons, I'd say Feynman is not being reasonably (a grey area!) clear here. Even a question mark after Δv in the figure would have gone a long way.

My rule for diagrams with examples of wrong way to do things is: always say so on the diagram.

I fully agree. It is inconsistent with what he did in figure 17-2 (attached). I guess I should report this to Michael Gottlieb, et al. I don't know how many new editions there will be. If a sufficient number of errors are reported, they might update the FLP again.

Feynman can't really be held responsible for the captioning of diagrams, or even the form in which they appear in print. That was the work of his colleagues.

It really is important to get things correct in a physics textbook. Even "trivial" things such as this diagram. There were some errors in previous editions that caused me considerable confusion. The FLP was my primary source when learning physics. I still recall sitting in my taxicab in between fares, agonizing over not understanding his presentation on gravitational potential energy, only to come to realize (years later) that it had errors in it.

 

[Hetware]

I wasn't referring to this being corrected specifically, I was just stating a rule of thumb. If I had requested for a dead man to make textbook corrections, your joke might have been more fitting ;)

There have been extensive revisions of the FLP over they years. I've reported a number of outstanding errors that are now corrected.

Here are the latest errata:

http://www.feynmanlectures.info/errata/FLP_New_Millennium_Edition_Newly_Reported_Vol_I_Errata.pdf

There have been at least 1156 corrections since the original publication.

 

[Hetware]

Am I correct that the representation in Fig. 11-7 amounts to the following:

$\Delta \pmb{v} \approx \pmb{\bar{v}} \Delta t+\pmb{a} \Delta t$,

and thus the incorrect result:

$lim_{\Delta t \rightarrow 0 } \frac{\Delta \pmb{v}}{ \Delta t} = \pmb{v} +\pmb{a}$

 

[Hetware]

Here's an example: let $\pmb{p}$ be the terminus of the velocity vector for a point on the unit circle moving at speed $\omega$.

$\pmb{p}=\pmb{r}+\pmb{v}$

$\pmb{r}=\{\cos \omega t,\sin \omega t\}$

$\pmb{v}=\omega \{-\sin \omega t,\cos \omega t\}$

$\pmb{p}=\{\cos \omega t,\sin \omega t\}+\omega \{-\sin \omega t,\cos \omega t\}$

$\pmb{\dot{p}}=\omega \{-\sin \omega t,\cos \omega t\}-\omega ^2\{\cos \omega t,\sin \omega t\}$

$\pmb{\dot{p}}=\pmb{v}+\pmb{a}$

 

[Hetware]

Could someone please verify what I have presented. I have been told that it is not correct. I am quite convinced that it is correct.

 

[Hetware]

Here is a depiction of the equivalent figure using my example. Notice that the $\Delta\vec{v}$ corresponding to Fig 11-7 (depicted in red) is always parallel to a tangent to the circle. It will never point in the correct direction of the acceleration $lim_{\Delta t \rightarrow 0}\frac{\Delta\vec{v}}{\Delta t}$ ($\Delta\vec{v}$ depicted in green.)

I'm hoping the person I am corresponding with will come to realize this.

I now realize that the figure is even more incorrect than I originally thought it was.

 

[Hetware]

Quod Erat Demonstrandum

 

[Andrew Mason]

Here is a depiction of the equivalent figure using my example. Notice that the $\Delta\vec{v}$ corresponding to Fig 11-7 (depicted in red) is always parallel to a tangent to the circle. It will never point in the correct direction of the acceleration $lim_{\Delta t \rightarrow 0}\frac{\Delta\vec{v}}{\Delta t}$ ($\Delta\vec{v}$ depicted in green.)

I'm hoping the person I am corresponding with will come to realize this.

I now realize that the figure is even more incorrect than I originally thought it was.

The whole point of Feynman's two diagrams and his explanation was to show that a common mistake is to do exactly what you are doing!

I don't understand why you are saying that the velocity vector is $\vec{v} + \vec{a}$. The dimensions of v and a are different, for one thing. Furthermore, the velocity vectors are always TANGENTIAL to $\vec{r}$ which is the radius of curvature of the path of the body.

The change in velocity is in the radial direction if you make the Δθ small enough: ie.

$$\vec{a} = \lim_{\Delta t\rightarrow 0} \frac{\Delta \vec{v}}{\Delta t} = -|a|\hat{r}$$

where $\hat r$ is the unit vector in the radial (outward) direction.

BUT you have to do the vector subtraction by moving the two velocity vectors so their tails are at the same point. That was Feynman's point, as shown in his subsequent diagram.
AM