Finding Coordinates of A and B in an Equilateral Triangle

[adjacent]

Homework Statement

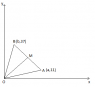
The points O,A and B are vertices of an equilateral triangle. Find a and b
O=(0,0)
A=(a,11)
B=(b,37)

Homework Equations

$c^2=a^2+b^2$

The Attempt at a Solution

Let AB =c
Then $c=\sqrt{(a-b)^2+(11-37)^2}=\sqrt{(a-b)^2+676}$
Since it is an equilateral triangle, OA and OB is also =c
So $c=\sqrt{11^2+a^2}$
$c=\sqrt{37^2+b^2}$
$\sqrt{(a-b)^2+676}=\sqrt{11^2+a^2}=\sqrt{37^2+b^2}$
I have got to know that $a^2+b^2=1248$, but what next?
I need to find at least one variable to find the other.

 

[ehild]

You have two independent equations:
$\sqrt{(a-b)^2+676}=\sqrt{11^2+a^2}$ and
$\sqrt{(a-b)^2+676}=\sqrt{37^2+b^2}$, for example.

Square the equations, and solve for a, b.


ehild

 

[Jilang]

You've used two equations for the length of c. There is a third one, can you see it?

 

[ehild]

You've used two equations for the length of c. There is a third one, can you see it?

It is not independent of the other two.

ehild

 

[adjacent]

I have a question.
Why is squaring both sides the same as multiplying both sides by something?
For example,we have an equation such that $a=b$
If we multiply both sides, the equation remain unchanged, $2a=2b$ --> $a=2b/2$--> $a=b$
Again we have an equation such that $a=2b$
If we square both sides, --> $a^2=(2b)^2$ --> $a \times a=2b \times 2b=4 \times b \times b$ --> $a=(4 \times b \times b)/a$

If I do it another way,it remains unchanged: $a=2b$--> $a^2=(2b)^2$ --> $a=\sqrt{(2b)^2}$--> $a=2b$

 

[ehild]

Squaring both sides of an equation is not the same as multiplying both sides with something. The equation stays true, but squaring might introduce false roots. You have to check at the end.
How would you isolate the unknowns without squaring?
If you have the equation a=b and you square both sides, a²=b², you can isolate one variable by taking the square roots. You get the solution a=±b. a=-b is false.

ehild

 

[adjacent]

Ok, nevermind

I have got this result after rearranging,squaring etc.
$b^2-2ab+676=11^2$
$a^2-2ab+676=37^2$

Before solving the simultaneous equation,I strongly believe this should become
$b^2=11^2$
$a^2=37^2$
but I don't know how. It's not possible to just cancel out the terms since they do not have opposite signs.

 

[ehild]

Check. Plug in the values and see what you get.

ehild

 

[adjacent]

Check. Plug in the values and see what you get.

ehild

It's wrong -_-
I have never solved equations of this kind. I don't know what to do when I have 3 variables($-2ab,b^2 and a^2$) . Any hints?

 

[ehild]

You have two unknowns, a and b. Isolate b from the second one and substitute the expression for b into the first one. Yo get an equation for a alone.

ehild

 

[adjacent]

I got a wrong answer:
$b=\frac{a^2-693}{2a}$
$a^2-2a. \left(\frac{a^2-693}{2a} \right)+676=37^2$
Solving for a, we get $a \in R$

 

[ehild]

You substituted back into the same equation.

$b=\frac{a^2-693}{2a}$
Substitute into
$b^2-2ab+676=11^2$

ehild

 

[adjacent]

You substituted back into the same equation.

$b=\frac{a^2-693}{2a}$
Substitute into
$b^2-2ab+676=11^2$

ehild

Ah,
I get the answer as
a=36.37
b=8.66

I solved this using my computer, I should do it myself too. Let me try:
Isolating b
$a^2-2ab=693$
$b=\frac{693-a^2}{-2ab}$
$=\frac{a^2-693}{2a}$

Plug it into the first equation
$b^2-2ab+676=121$
$\left(\frac{a^2-693}{2a} \right)^2-2a\left(\frac{a^2-693}{2a} \right)=-555$
After doing many steps, I got to this:$$-3a^4+3606a^2+480249=0$$

I am not sure what I should do after this step , some kind of 4th power equation?

 

[SteamKing]

Look carefully at the equation you wind up with. It's a quadratic in a^2.

 

[adjacent]

Look carefully at the equation you wind up with. It's a quadratic in a^2.

Why should it be a quadratic equation? We have a $-3a^4$ there.

 

[Ray Vickson]

Why should it be a quadratic equation? We have a $-3a^4$ there.

You really don't see what you get when you put $a^2 = x$?

 

[adjacent]

You really don't see what you get when you put $a^2 = x$?

oh, I never thought of it :shy:
This is the first time I have solved such a scary equation-Feeling happy
Thanks guys

btw, can't we solve it using elimination method?

 

[Ray Vickson]

oh, I never thought of it :shy:
This is the first time I have solved such a scary equation-Feeling happy
Thanks guys

btw, can't we solve it using elimination method?

Standard trick. Whenever you have an equation in even powers $a^{\pm 2k}$ you can put $a^2 = x$ and get an equation involving $x^{\pm k}$.

As for 'elimination': yes, you can use the equality $a^2 + 11^2 = b^2 + 37^2$ to write $b$ in terms of $a$. Since your drawing indicates $b \geq 0$ there will not (at this stage) be a problem of choosing the correct sign: $b = \sqrt{a^2 - 1248}$. Put that into the equation $a^2 + 11^2 = (a-b)^2 + 676$, so you have eliminated $b$. However, the result is not a very nice equation for $a$.

 

[adjacent]

No. I mean can we use the elimination method for solving these two equations?(Simultaneous equation)
$(a-b)^2+676}=11^2+a^2$
$(a-b)^2+676=37^2+b^2$

 

[Saitama]

There is a much shorter solution. Use complex numbers. :)

Do you see that the following equation holds?

$$b+37i=(a+11i)e^{i\pi/3}$$

Just compare the imaginary and real parts.

 

[Ray Vickson]

No. I mean can we use the elimination method for solving these two equations?(Simultaneous equation)
$(a-b)^2+676=11^2+a^2$
$(a-b)^2+676=37^2+b^2$

(Error corrected above---you had an unmatched '}').

Which message are you responding to? Please use the 'quote' button, so such confusion is eliminated.

My previous post did, indeed, show how to use the 'elimination' method on those very two equations. However, it first used the fact that the two right-hand-sides are equal---because the left-hand-sides are---to get an equation that makes the elimination much, much easier.

 

[ehild]

There is a much shorter solution. Use complex numbers. :)

Do you see that the following equation holds?

$$b+37i=(a+11i)e^{i\pi/3}$$

Just compare the imaginary and real parts.

It is very clever, Pranav!

ehild

 

[Saitama]

It is very clever, Pranav!

ehild

Thank you, sir!

 

[thelema418]

I have a question.
Why is squaring both sides the same as multiplying both sides by something?
For example,we have an equation such that $a=b$
If we multiply both sides, the equation remain unchanged, $2a=2b$ --> $a=2b/2$--> $a=b$
Again we have an equation such that $a=2b$
If we square both sides, --> $a^2=(2b)^2$ --> $a \times a=2b \times 2b=4 \times b \times b$ --> $a=(4 \times b \times b)/a$

If I do it another way,it remains unchanged: $a=2b$--> $a^2=(2b)^2$ --> $a=\sqrt{(2b)^2}$--> $a=2b$

I think about "squaring both sides" in terms of multiplication with substitution. In your example you have $a = 2b$. If we multiply the equation by $a$, and this yields $a \cdot a = a (2b)$. We can substitute the $a$ on the right-hand side of the equation with $a = 2b$. Now, $a\cdot a = (2b)\cdot (2b)$, or simply $a^2 = (2b)^2$.

Note that where you wrote , you can substitute $a = 2b$. Then $a = (4 \times b \times b) / 2b = 2b$.

I hope that helps.

 

[adjacent]

There is a much shorter solution. Use complex numbers. :)

Do you see that the following equation holds?

$$b+37i=(a+11i)e^{i\pi/3}$$

Just compare the imaginary and real parts.

It is very clever, Pranav!

ehild

It's very clever but it's far too advanced for me
Ray Vickson, I am asking whether Elimination method can be used for solving the two simultaneous equation. I used the substitution method where we solved the second equation for b and substituted it in the first equation.
In the elimination method,we do this:
If we have two equations $x+y=1$ and $x-y=3$
We multiply the coefficient of the first term in the first equation with the second equation and vice versa.
I am having trouble here because the first two terms are different and the $b^2$,$a^2$ and $-2ab$ seems to act like three different variables. Hope you understand what I am trying to say

 

[adjacent]

I think about "squaring both sides" in terms of multiplication with substitution. In your example you have $a = 2b$. If we multiply the equation by $a$, and this yields $a \cdot a = a (2b)$. We can substitute the $a$ on the right-hand side of the equation with $a = 2b$. Now, $a\cdot a = (2b)\cdot (2b)$, or simply $a^2 = (2b)^2$.

Note that where you wrote , you can substitute $a = 2b$. Then $a = (4 \times b \times b) / 2b = 2b$.

I hope that helps.

I see, that helped. Thanks

 

[ehild]

It's very clever but it's far too advanced for me

Haven't you studied complex numbers yet?

Or have you studied how the components of a vector change when turned by an angle θ round the origin?

Or the summation laws for trigonometric functions?


ehild

 

[adjacent]

Haven't you studied complex numbers yet?

Yes

Or have you studied how the components of a vector change when turned by an angle θ round the origin?

No. But I think it's pretty obvious.It's just a right angle triangle whose hypotenuse's length remains constant. So I can use that fact to find the other two sides.

Or the summation laws for trigonometric functions?

I think I know two of them.
$\sin(a+b)=\sin(a)\cos(b)+\cos(a)\sin(b)$
$\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$
Heared it from a calculus lecture I watched some days ago

 

[ehild]

Yes

No. But I think it's pretty obvious.It's just a right angle triangle whose hypotenuse's length remains constant. So I can use that fact to find the other two sides.

I think I know two of them.
$\sin(a+b)=\sin(a)\cos(b)+\cos(a)\sin(b)$
$\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$
Heared if from a calculus lecture I watched some days ago

Very good. Look at the picture. You find two right triangles, the red one having angle Φ with the x axis, the blue one has angle θ. θ=60°+Φ.
If the sides of the equilateral triangle are of length C, C cos(θ)=b, C sin(θ)=37 Ccos(Φ)=a, Csin(Φ)=11

θ=60°+Φ, apply the addition laws. You know that cos60°=1/2, sin/°=√3/2.

Csin(60°+Φ)=Csin(60°)cos(Φ)+Ccos(60°)sin(Φ)→(√3/2)a+(1/2)11=37

Do the same with Ccos(θ):

C cos(60°+Φ)=Ccos(60°)cos(Φ)-Csin(60°)sin(Φ)→(1/2) a-(√3/2)11=b

Solve.


ehild

 

[adjacent]

θ=60°+Φ

How do you know this?
EDIT: Oh I got it, How dumb I am !

This also yields a simultaneous equation right?
Anyway, thank you so much! I learned a lot from this thread. Thanks everyone!

 

[ehild]

This also yields a simultaneous equation right?
Anyway, thank you so much! I learned a lot from this thread. Thanks everyone!

It yields the equations in bold in my previous post. See if you get the same ones, by applying the summation laws.

The equations are very easy to solve: There is only one unknown, a, in the first one.


ehild

 

[adjacent]

It yields the equations in bold in my previous post. See if you get the same ones, by applying the summation laws.

The equations are very easy to solve: There is only one unknown, a, in the first one.

I get the same thing too. Thanks for helping me.

 

[sankalpmittal]

It can be also done by using Coni's method. BTW, adjacent you're 15 ?

 

[thelema418]

I just want to point out that this problem has two possible solutions: I only saw one posted. You can see this by drawing lines to represent the possible points for A and B. In other words, $(a, 11)$ is somewhere on the line $y = 11$. The point $(b, 37)$ is somewhere on the line $y = 37$. Since the distance from O to A and from O to B is the same, we can draw a circle with radius $r$ and center at O. The intersections show the possible solutions. One is in QI and the other is in QII.

 

[sankalpmittal]

I just want to point out that this problem has two possible solutions: I only saw one posted. You can see this by drawing lines to represent the possible points for A and B. In other words, $(a, 11)$ is somewhere on the line $y = 11$. The point $(b, 37)$ is somewhere on the line $y = 37$. Since the distance from O to A and from O to B is the same, we can draw a circle with radius $r$ and center at O. The intersections show the possible solutions. One is in QI and the other is in QII.

Yes, by distance formula it's obvious that there are two solutions. To reduce the calculation part, I preferred Coni's method(in complex numbers), which also offers two solutions.z₁/z₂= e^iπ/3

In this case |z₁|=|z₂|...being an equilateral triangle.