Finding Accel. of Particle: t1=2s t2=5s | Mean Accel.

[JaySean]

1. Not sure if it's the right forum but I'll try. The velocity of an particle varies quadratic with a formula based on time

a) Find the equation for acceleration and length as a function of time.
b) a = 3 m/s^3 (I think it's alpha)
Find the acceleration when t1=2s t2=5s and how big is the mean acceleration in the time intervall t2-t1.

2. See picture3. a) I think you can use the formula

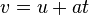saying u=0 (start velocity) and say a=(v-u)/t
And do the same for

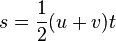where s= length. But is it that easy or are they looking for a different solution, as this is something I learned few years ago. Or do I have to antiderivate it, which would make it complicated because there is no known fact.

b) If a) is right could I then say solve v(t) which gives me t=3 alpha= 3 --> v(t)=27 m/s, and then get acceleration by the 2nd formula

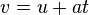v= 27 u=0 t=3, so acceleration is 9? Or am I on the wrong way?

 

[Doc Al]

The velocity of an particle varies quadratic with a formula based on time

That's a bit vague. Is any additional information given? Such as velocity at time 0.

I think you can use the formula

saying u=0 (start velocity) and say a=(v-u)/t

Careful! Those formulas are for constant acceleration, which is not what you have here. (Note how the velocity is linear with time, not quadratic, in the formula.)

Hint: Calculus made be involved.

 

[JaySean]

That's a bit vague. Is any additional information given? Such as velocity at time 0.Careful! Those formulas are for constant acceleration, which is not what you have here. (Note how the velocity is linear with time, not quadratic, in the formula.)

Hint: Calculus made be involved.

There is no additional information, but the formula (picture).

Do you have any hint to how I get started on solving b)?

 

[Doc Al]

There is no additional information, but the formula (picture).

Ah, I see it now. $v(t) = 1/2 \alpha t^2$.

Do you have any hint to how I get started on solving b)?

First solve part a).

 

[JaySean]

Do I have to solve it as differintial equation? As I'm not allowed to use the formula for constant accerlation?

I know I can derivate v'(t) to get a(t)= at where a= alpha, but how do get to the length formula?

 

[Doc Al]

Do I have to solve it as differintial equation?

You'll have to use a bit of calculus. (How do distance, velocity, and acceleration relate to each other?)

As I'm not allowed to use the formula for constant accerlation?

That's correct. You cannot use the standard constant acceleration formulas here.

 

[JaySean]

I know that the distance particle traveled is s(t)= antiderivative of v(t), but wouldn't I need additional information to find the constant?

Edit: Already found the formula for acceleration a(t)= qt where q is a constant

 

[HallsofIvy]

I know that the distance particle traveled is s(t)= antiderivative of v(t), but wouldn't I need additional information to find the constant?

Not to find the distance traveled over a given time interval. That is the difference between two lengths

Edit: Already found the formula for acceleration a(t)= qt where q is a constant

 

[Doc Al]

I know that the distance particle traveled is s(t)= antiderivative of v(t), but wouldn't I need additional information to find the constant?

To express the position, you'd need additional info. But for the distance traveled, you can just set s(t=0) = 0.

Edit: Already found the formula for acceleration a(t)= qt where q is a constant

Good. (That constant is given as $\alpha$.)

 

[JaySean]

To express the position, you'd need additional info. But for the distance traveled, you can just set s(t=0) = 0.Good. (That constant is given as $\alpha$.)

(I didn't know how to write alpha so I just called it q)
So the formula for poisition as a function of time is S(t)=0 when t=0?

and for b) since a(t)=qt where q=3 m/s^3 for t1= 2s and t2=5s
a(2)=6 m/s^2 and a(5)=15 m/s^2
mean accleration= 11/3 m/s^2

 

[Doc Al]

(I didn't know how to write alpha so I just called it q)
So the formula for poisition as a function of time is S(t)=0 when t=0?

Yes, that will give you the position from the starting point (where t = 0, presumably).

and for b) since a(t)=qt where q=3 m/s^3 for t1= 2s and t2=5s
a(2)=6 m/s^2 and a(5)=15 m/s^2

Good.

mean accleration= 11/3 m/s^2

How did you calculate that?

 

[JaySean]

How did you calculate that?

Sorry I meant 21/3 m/s^2 which is 7m/s^2
a(2)+a(5) =6+15=21
And t2-t1=5-2=3

 

[Doc Al]

Sorry I meant 21/3 m/s^2 which is 7m/s^2
a(2)+a(5) =6+15=21
And t2-t1=5-2=3

Careful! What's the definition of average acceleration?

 

[JaySean]

Careful! What's the definition of average acceleration?

Since I already know what alpha is and time is I might be able to use the general formula for acceleration knowing the velocity at beginning and end.
This gives me
vo=3*(2)^2=12
v1=3*(5)^2=75

acceleration= (75-12)/(5-2)=21

 

[Doc Al]

Since I already know what alpha is and time is I might be able to use the general formula for acceleration knowing the velocity at beginning and end.

Good.

This gives me
vo=3*(2)^2=12
v1=3*(5)^2=75

You left out the factor of 1/2.

 

[JaySean]

Sorry this is stupid of me,
(37,5-6)/3 =10,5
v1-v0/delta(t)

I have another question not sure if anyone is able to answer:

Car with velocity 36 km/h colliding and stoping over a length of 1 meter (end velocity = 0). Find acceleration.
I have solved it the simple way using v^2 = u^2 + 2as and got the right answer.
Now my question is how do I set it up as an differential equation.

My attempt:
Since I know S(0)= 1 (saying start position is 1 and end is 0)
velocity start = 36km/h and end is 0
I also know that position is antiderivative of velocity
S(t)=∫36
S(t)= 36t+C

Attempt on finding constant c.
S(0)=36*0+C=1
C= 1
S(t)= 36t+1

 

[Doc Al]

My attempt:
Since I know S(0)= 1 (saying start position is 1 and end is 0)

I would say that the start position is 0 and the end position is 1.

I also know that position is antiderivative of velocity
S(t)=∫36

You cannot assume that the velocity is constant. (After all, you are told that it is stopping.)

All you'll do, by setting up a differential equation, is derive those kinematic formulas. Nothing wrong with that, as long as you start with the correct assumptions. Assume that the acceleration is constant, then you can integrate to get the position as a function of time.

 

[JaySean]

All you'll do, by setting up a differential equation, is derive those kinematic formulas. Nothing wrong with that, as long as you start with the correct assumptions. Assume that the acceleration is constant, then you can integrate to get the position as a function of time.

Do you mean derivating for example the formula
v=v0+at?

 

[Doc Al]

Do you mean derivating for example the formula
v=v0+at?

Yes. And, using a few tricks, all the others.