- #1
Fontseeker
- 30
- 4
I have the following problem:
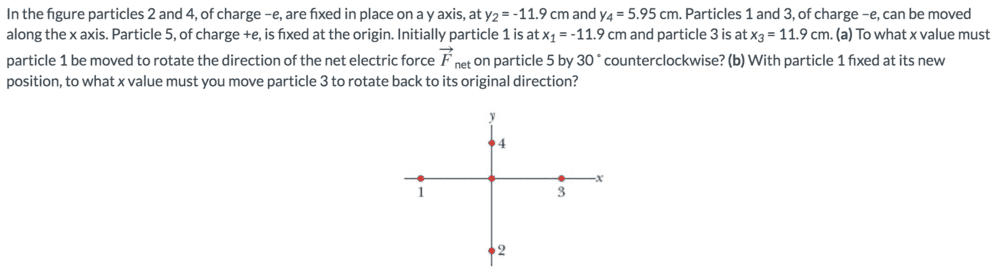
So, I know the following:
##q_1 = -e##
##q_2 = -e##
##q_4 = -e##
##q_5 = e##
##e = 1.6*10^{-19}##
##k = 9*10^{9}##
Now, I can get the current ##F_{net}## of particle 5 with this information:
##F_{net} = (F_{3} - F_{1})\hat i + (F_{2} + F_{4})\hat j##
##F_{1} = k * \frac{e * e}{x_1^2} = 1.627 * 10^{-26}N##
##F_{2} = k * \frac{e * e}{y_2^2} = 6.508 * 10^{-26}N##
##F_{3} = k * \frac{e * e}{x_3^2} = 1.627 * 10^{-26}N##
##F_{4} = k * \frac{e * e}{y_4^2} = 1.627 * 10^{-26}N##
Now, I can break up ##F_{net}## into components:
##F_{x} = (1.627 * 10^{-26} - 1.627 * 10^{-26})N =0N##
##F_{y} = (6.508 * 10^{-26} - 1.627 * 10^{-26})N = 4.881 * 10^{-26}N##
To rotate ##F_{net}## by 30 degrees, I know the y component will not change, so I can make this assumption:
##\tan \theta= \frac{F_x}{F_{y}}##
so
##{F_x} = \tan \theta * F_{y} = \tan 30 * 4.881 * 10^{-26}N = 2.818 * 10^{-26}N##
and since it is rotating counterclockwise, the x component must be negative:
##{F_x} = -2.818 * 10^{-26}N##
Now, to find the new position, r, of particle 1 to get this new ##{F_x}## for the net charge of particle 5
##{F_x} = {F_3} - {F_1}##
##{F_1} = {F_3} - {F_x}##
##{F_1} = {F_3} - {F_x}##
##k * \frac{e * e}{r^2} = {F_3} - {F_x}##
##r = \sqrt {\frac{k * e * e}{{F_3} - {F_x}}}##
##r = \sqrt {\frac{k * e * e}{1.627 * 10^{-26} - (-2.818 * 10^{-26})}}##
##r = \sqrt {\frac{k * e * e}{1.627 * 10^{-26} + 2.818 * 10^{-26}}}##
##r = 0.071995m##
So, the new position of particle 1 is at (0.071995m, 0), which is my answer for part A. Now, for part B, the new position of particle 3 would have to be (-0.071995m, 0). However, this is the wrong answer. Does anyone see my mistake?
So, I know the following:
##q_1 = -e##
##q_2 = -e##
##q_4 = -e##
##q_5 = e##
##e = 1.6*10^{-19}##
##k = 9*10^{9}##
Now, I can get the current ##F_{net}## of particle 5 with this information:
##F_{net} = (F_{3} - F_{1})\hat i + (F_{2} + F_{4})\hat j##
##F_{1} = k * \frac{e * e}{x_1^2} = 1.627 * 10^{-26}N##
##F_{2} = k * \frac{e * e}{y_2^2} = 6.508 * 10^{-26}N##
##F_{3} = k * \frac{e * e}{x_3^2} = 1.627 * 10^{-26}N##
##F_{4} = k * \frac{e * e}{y_4^2} = 1.627 * 10^{-26}N##
Now, I can break up ##F_{net}## into components:
##F_{x} = (1.627 * 10^{-26} - 1.627 * 10^{-26})N =0N##
##F_{y} = (6.508 * 10^{-26} - 1.627 * 10^{-26})N = 4.881 * 10^{-26}N##
To rotate ##F_{net}## by 30 degrees, I know the y component will not change, so I can make this assumption:
##\tan \theta= \frac{F_x}{F_{y}}##
so
##{F_x} = \tan \theta * F_{y} = \tan 30 * 4.881 * 10^{-26}N = 2.818 * 10^{-26}N##
and since it is rotating counterclockwise, the x component must be negative:
##{F_x} = -2.818 * 10^{-26}N##
Now, to find the new position, r, of particle 1 to get this new ##{F_x}## for the net charge of particle 5
##{F_x} = {F_3} - {F_1}##
##{F_1} = {F_3} - {F_x}##
##{F_1} = {F_3} - {F_x}##
##k * \frac{e * e}{r^2} = {F_3} - {F_x}##
##r = \sqrt {\frac{k * e * e}{{F_3} - {F_x}}}##
##r = \sqrt {\frac{k * e * e}{1.627 * 10^{-26} - (-2.818 * 10^{-26})}}##
##r = \sqrt {\frac{k * e * e}{1.627 * 10^{-26} + 2.818 * 10^{-26}}}##
##r = 0.071995m##
So, the new position of particle 1 is at (0.071995m, 0), which is my answer for part A. Now, for part B, the new position of particle 3 would have to be (-0.071995m, 0). However, this is the wrong answer. Does anyone see my mistake?
Last edited by a moderator: