Finding the magnetic field at a point P

[bfusco]

Homework Statement

Im reviewing for a test so I am doing some practice questions. need help with this one.

The questions simply states "find the magnetic field at point P for the steady current configurations shown below.

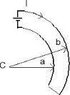
Because i cannot find the exact picture on the internet i am going to attempt to describe the setup, and provide a picture of a similar setup.

If you were to imagine the x and y axis, the origin is the point P where the magnetic field is desired to be known. The current carrying loop consists of a quarter circle of radius a, and another larger quarter circle radius b. Both quarter circles are in the same quadrant. The 2 circles are connected by straight edges, which lay on the axis and the current circulates clockwise.

The Attempt at a Solution

I understand that the magnetic field from the straight edges on the axis will not contribute to the magnetic field at P.

I understand also that the magnetic field at P generated by the quarter circle with radius a, will point out of the page, and the quarter circle with radius b will point into the page, however since the quarter circle with radius a is closer than the quarter circle with radius b, the magnitude of the magnetic field due to a is greater than that of b. Therefore, the total B field will point out of the page.

Im having a hard time understanding how to apply the biot savart law to this one.

 

[hjelmgart]

Biot and Savarts law describes the strength of the magnetic field in a single point, P.

So you simply find the strength for wire a, and for wire b, and you add them. (one of them should be negative of course)

EDIT:

For a wire as this one, it could be a bit tricky, as it depends on the location of your point, P. The figure you attached, is it supposed to show, that the point is in the center of the circle? Sincethen you have contribution from the entire wire in that point.

 

[bfusco]

thanks for the response.

I understand what you have mentioned, my issue is actually using the Biot-savart law to find the magnitude. I am unsure how to apply it to to a point at the center of a circle.
$$B(r)=\frac{\mu_0}{4\pi}I \int dl' \times \hat{r}\frac{1}{r^2}$$

I don't know how to determine $\hat{r}$ and the magnitude $\frac{1}{r^2}$ for a quarter circle. Since the point we're interested in is at the origin, i can't use the geometrical interpretation where $r=r_{field}-r_{source}$

 

[hjelmgart]

Yeah, I can relate, however, it can be quite simple actually!

The cross product is quite simple, since the unit vector always points towards the center of the circle, it just becomes dl' sin(90) since the

Then you only have to integrate over the path, dl', which is simply the circumference.

 

[bfusco]

For a wire as this one, it could be a bit tricky, as it depends on the location of your point, P. The figure you attached, is it supposed to show, that the point is in the center of the circle? Sincethen you have contribution from the entire wire in that point.

the point P is close to where C is in that picture provided.

If you draw 2 circles one with radius 'a' and the other 'b' and center those on the origin, then erase the parts of the circles in quadrants 2,3,4, you're left with 2 quarter circles in quadrant 1. Point P would be at the origin of the axis. If you then connect those as is done in the picture, you have the setup i am attempting to describe.

 

[hjelmgart]

As long as the point P, is at the center of the circle, it should be simple.

So you follow the cross product thing? Since you take the cross product between the vector l', which is the same direction as the current.

So circle with radius a has sin(90) and circle radius b has sin(-90).

You then add the two values, you obtain with Biot and Savarts law, where one becomes negative due to the sin(-90)

 

[Simon Bridge]

Just wondering if the problem does not have a simple relationship to the B magnitude from a complete current loop?
Which is something that would have been calculated in class.
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/curloo.html

 

[hjelmgart]

[Perhaps I didn't make it very clear :-)

I don't know how to determine $\hat{r}$ and the magnitude $\frac{1}{r^2}$ for a quarter circle. Since the point we're interested in is at the origin, i can't use the geometrical interpretation where $r=r_{field}-r_{source}$

The $\hat{r}$ is just a unit vector, its magnitude is one. The cross product between dl' and $\hat{r}$ is simply the magnitudes of each vector times sine to the angle between them.

The direction of dl' is the same as the direction of the current. So the angle between it and $\hat{r}$ will be 90 degrees for the inner circle and -90 for the outer.

And you know $\frac{1}{r^2}$, because it is simply the radius of the circle. It doesn't matter if it's a quarter circle.

The only thing affected by the fact, that it is a quarter circle, is the $\int dl'$, since that integral gives the length of the wire, you want to know the magnetic field at the point P, for.

As I said earlier, you can simply do Biot and savarts law twice. One for the inner wire, and one for the outer wire. Then you can add them, and you have the magnitude of the magnetic field at the point B.

Also $r=r_{field}-r_{source}$ is not wrong, but since you have your point in origo, it is just the radius. However, you can always place your point elsewhere in the coordinate system. As long as you move the wires accordingly. Then you will get the same result. It's just placed in origo for making it simpler. In fact you can always place it origo even if the assignment doesn't say, where it is placed. It makes the problem easier, when you are dealing with a circle.

 

[Blakely42]

Just want to say this was an immensely helpful explanation for me. Thank you!

 

[Blakely42]

This is a great explanation of the problem. It helped a ton that you stated what you did understand, since I also was struggling with the same problem, and understood it at the same level as you.