Energy Losses in a Circuit with a Switching Element

[Ivan Antunovic]

Homework Statement

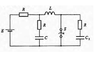
By the time t = 0 network has been in steady state. At time t = 0, the switch S
switches off. Determine the total amount of energy converted to heat in the circle of resistance to the establishment of a new steady state.

Homework Equations

[/B]

The Attempt at a Solution

Picture,attached.
Okay before the switch is opened, both C and C2 are short circuited,so initial current i(0)=E/R.
So I had this approach,okay let's find voltages on the capacitors vc(t) and from ic(t) = C* dv/dt , I will get a current and then it's easy to find the energy since it's integral of i*R^2 *dt (from 0 to infinity).
I wrote down KCLs and KVLs,and used laplace transform,but things got really complicated,I think my approach isn't right(atleast not the shortest one).
Are those laplace transforms that I wrote,even correct?

 

[gneill]

Your images do not identify where the switch is located. Also, it is difficult to read and comment on workings in image form. It is much preferable to type them out so that helpers can quote and comment on individual lines. The built-in LaTeX syntax interpretation of PF can help there.

For this type of problem where you're looking for the energy dissipated between two steady states, it generally suffices to find the stored energy in each of the steady states and take the difference. So the first thing to do is identify the conditions at each of the steady states.

 

[Ivan Antunovic]

Your images do not identify where the switch is located. Also, it is difficult to read and comment on workings in image form. It is much preferable to type them out so that helpers can quote and comment on individual lines. The built-in LaTeX syntax interpretation of PF can help there.

For this type of problem where you're looking for the energy dissipated between two steady states, it generally suffices to find the stored energy in each of the steady states and take the difference. So the first thing to do is identify the conditions at each of the steady states.

I forgot to upload a picture,it was very late so I guess that's the reason,sorry.
So before the switch is opened:
We have both R and C2 short circuited,initial current is $$i(-0)= E/R$$,no current goes through a capacitor so i(-0) is actually current going through inductor,so stored energy in inductor is $$WL(-0)=0.5 * L* (i(-0))^2 = 0.5 * L * (E/R)^2$$ ,okay now if I make KVL for a first loop ,I get $$+E-i(-0)*R-vc(-0)=0$$,therefore
$$vc(-0)=E-i(-0)*R= E-R*(E/R)=E-E=0$$,which was obvious since there is no induced voltage since we are dealing with DC current(I am not quite sure If I can say 'no voltage drop across inductor',since physicists going to kill me because there is never electric field in the ideal inductor so equation ,integral of E*dl = 0 cannot be applied).
After the switch is opened and after the transient process is over,there is no current flowing, because both C and C1 are charged and they are connected in parallel since no voltage drop on the resistances,and inductor is a short circuit here,and I get Vc(infinity)=Vc2(infinity)=E.
Therefore stored energy in the capacitors $$Wc(infinity)=0.5 * C * E^2 , Wc1(infinity)=0.5*C1*E^2.$$$$\Delta E=( (0.5*E^2)*(C+C1) ) - (0.5*L (E/R)^2 ) = 0.5 * E^2 (C+C1-(L/R^2))$$

Should this be okay?

 

[Ivan Antunovic]

I forgot to upload a picture,it was very late so I guess that's the reason,sorry.
So before the switch is opened:
We have both R and C2 short circuited,initial current is $$i(-0)= E/R$$,no current goes through a capacitor so i(-0) is actually current going through inductor,so stored energy in inductor is $$WL(-0)=0.5 * L* (i(-0))^2 = 0.5 * L * (E/R)^2$$ ,okay now if I make KVL for a first loop ,I get $$+E-i(-0)*R-vc(-0)=0$$,therefore
$$vc(-0)=E-i(-0)*R= E-R*(E/R)=E-E=0$$,which was obvious since there is no induced voltage since we are dealing with DC current(I am not quite sure If I can say 'no voltage drop across inductor',since physicists going to kill me because there is never electric field in the ideal inductor so equation ,integral of E*dl = 0 cannot be applied).
After the switch is opened and after the transient process is over,there is no current flowing, because both C and C1 are charged and they are connected in parallel since no voltage drop on the resistances,and inductor is a short circuit here,and I get Vc(infinity)=Vc2(infinity)=E.
Therefore stored energy in the capacitors $$Wc(infinity)=0.5 * C * E^2 , Wc1(infinity)=0.5*C1*E^2.$$$$\Delta E=( (0.5*E^2)*(C+C1) ) - (0.5*L (E/R)^2 ) = 0.5 * E^2 (C+C1-(L/R^2))$$

Should this be okay?So basically that difference of energy in reactive elements is always lost energy,dissipated in the resistor?

 

[gneill]

I'm thinking about this. Not knowing the position of the switch initially, I thought perhaps the inductors and capacitors would end up isolated so that no new energy could enter the loop. But now I can see that there is the possibility of damped oscillations while the battery E continues to supply energy to charge the capacitors to their final value. I'm not sure that the difference in stored energy between the states will account for all the energy. Current can actually flow back through the battery during the oscillations, and current flowing in either direction still burns energy in the resistors.

I can also see that a complete solution via Laplace transforms will be messy since there are three separate energy storage devices. So I'm not sure what to recommend at the moment.

 

[Ivan Antunovic]

I'm thinking about this. Not knowing the position of the switch initially, I thought perhaps the inductors and capacitors would end up isolated so that no new energy could enter the loop. But now I can see that there is the possibility of damped oscillations while the battery E continues to supply energy to charge the capacitors to their final value. I'm not sure that the difference in stored energy between the states will account for all the energy. Current can actually flow back through the battery during the oscillations, and current flowing in either direction still burns energy in the resistors.

I can also see that a complete solution via Laplace transforms will be messy since there are three separate energy storage devices. So I'm not sure what to recommend at the moment.

Okay,found the solution and it's correct,well there will be damped oscillations since we have R,L and C,but it doesn't matter right?We only care about the final state of the network.

 

[gneill]

Okay,found the solution and it's correct,well there will be damped oscillations since we have R,L and C,but it doesn't matter right?We only care about the final state of the network.

That was my initial thought (which I'm happy to have confirmed), but I wish I could think of a theorem that proves that the oscillations don't matter here.. I hate being right but not knowing why

 

[Ivan Antunovic]

That was my initial thought (which I'm happy to have confirmed), but I wish I could think of a theorem that proves that the oscillations don't matter here.. I hate being right but not knowing why

Well,it's quite intuitive that oscillations don't matter here.I don't know about the mathematical proof,but I like to think more as an engineer than as a mathematician.Maybe some good physicist could help us about the theorem.