Finding the Force between a Straight Wire and a Triangular Current Loop

[The Head]

Homework Statement

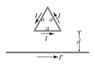
A triangular loop of side length a carries a current I. If this loop is placed a distance d away from a very long straight wire carrying a current I', determine the force on the loop. See attachment for diagram.

Homework Equations

F=($\mu$II'/2$\pi$r)L
F=I'LB
B=$\mu$I/2$\pi$r

The Attempt at a Solution

I broke the calculation into three pieces. Force on the horizontal portion of the triangle, and the force on each of the two diagonal pieces.

The force of the horizontal portion is just F=$\mu$II'*L/2$\pi$r

dB=$\mu$I dr/2$\pi$r
B=$\mu$I/2$\pi$ $\int$dr/r
The distance from the wire carrying I' ranges from d to d+a/$\sqrt{3}$. Thus, I set these as the limits of integration. Integrating I dr/r I get ln(r). Plugging this in with the appropriate limits, I get:
B=($\mu$I/2$\pi$)*(ln(1+a/d$\sqrt{3}$)

Because both horizontal elements are equal, I will use the total length = a and combine these two forces:
Diagonal Force=($\mu$II'/2$\pi$)*(ln(1+a/d$\sqrt{3}$)

Total force on the current element is the difference b/w the two forces:
Total Force=($\mu$II'/2$\pi$)*(a/d-(ln(1+a/d$\sqrt{3}$))
? Not sure what is wrong? Please help and thank you!

 

[anathema]

Thank you for your question. After reviewing your calculations, it seems that you may have made a small mistake in your integration. When integrating I dr/r, the correct result should be ln(r) + C, where C is a constant of integration. In this case, the constant of integration will be ln(d), since the limit of integration is from d to d+a/\sqrt{3}. Therefore, your final equation for B should be:

B = (\muI/2\pi)*(ln(d+a/d\sqrt{3}) - ln(d))

When plugging this into your equation for the diagonal force, you should get:

Diagonal Force = (\muII'/2\pi)*(ln(d+a/d\sqrt{3}) - ln(d))

Total force on the current element is the difference between the two forces:

Total Force = (\muII'/2\pi)*(a/d - (ln(d+a/d\sqrt{3}) - ln(d)))

Simplifying this further, we get:

Total Force = (\muII'/2\pi)*(a/d - ln(1+a/d\sqrt{3}))

I hope this helps to clarify your calculations. Please let me know if you have any further questions or if you need any additional assistance. Best of luck with your research!