Finding the moment of inertia

[hms.tech]

Homework Statement

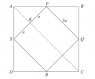
Two uniform square laminas are combined into a single body. One lamina ABCD has mass 5m and the other lamina PQRS has mass m. The lamina PQRS has side 2a, and its vertices are at the mid-points of the sides of ABCD, with P on AB and S on AD. The line PS meets AC at K, and the body rotates in a vertical plane about a horizontal axis k through K (see diagram). Find the moment of inertia of the body about k.

Homework Equations

parallel and the perpendicular axes theorems

The Attempt at a Solution

If i understand the question correctly, is the "dashed"(broken)line, the axis about which we need to find the moment of inertia ? If that is the case, here is what i did :Using the perpendicular axes theorem : (let $I_{A}$ be the moment of inertia about the required axis for ABCD only)
2$I_{A}$ = $\frac{5m(2a^{2}+2a^{2})}{3}$
$I_{A}$ = $\frac{10ma^{2}}{3}$

Similarly, let $I_{B}$ be the moment of inertia about the required axis for PQRS only :
Using the perpendicular axes theorem,
$I_{B}$ = $\frac{ma^{2}}{3}$

The total moment of inertia = $I_{A}$ + $I_{B}$
Total = $\frac{11ma^{2}}{3}$

The problem is that the solution notes state the answer to be $\frac{40ma^{2}}{3}$

 

[rude man]

Since k was not indicated on the diagram it's a bit of a puzzle all right as to what the axis of rotation is. It's supposed to be a "horizontal" axis which would seem to eliminate the dashed line though. I think the intended axis is a "hozizontal" line passing thru point K. In other words, the axis of rotation is parallel to line AB, and also to a line drawn thru SQ, and situated inbetween those two and passing thru point K.

Happy integration!

 

[haruspex]

I would interpret rotating "in a ... plane" as meaning the axis is perpendicular to the lamina.

 

[rude man]

I would interpret rotating "in a ... plane" as meaning the axis is perpendicular to the lamina.

That sounds sound. I agree.

 

[Nickie]

Your attempt at solving the problem using the perpendicular axes theorem is a good start. However, it is important to note that the axis of rotation in this problem is not a principal axis (i.e. parallel or perpendicular to one of the square laminas). Therefore, we cannot simply sum the moments of inertia of the two laminas using the perpendicular axes theorem.

To find the moment of inertia of the combined body, we need to use the parallel axes theorem. This theorem states that the moment of inertia of a body about any axis is equal to the moment of inertia about a parallel axis through the center of mass plus the product of the mass and the square of the distance between the two axes.

In this case, we can find the moment of inertia of the combined body about an axis through the center of mass (which is also the axis of rotation) using the parallel axes theorem. Then, we can add the moment of inertia of the two individual laminas about their respective axes (which you have already calculated using the perpendicular axes theorem). The final answer will be the sum of these three moments of inertia.

Here is the solution:

Let I_{CM} be the moment of inertia of the combined body about an axis through the center of mass.

Using the parallel axes theorem, we can write:
I_{CM} = I_{COM} + md^{2}

where I_{COM} is the moment of inertia of the combined body about an axis through the center of mass (which is equal to the sum of moments of inertia of the two laminas about their respective axes) and d is the distance between the two axes.

We can calculate I_{COM} by adding the moments of inertia of the two laminas about their respective axes:
I_{COM} = I_{A} + I_{B} = \frac{10ma^{2}}{3} + \frac{ma^{2}}{3} = \frac{11ma^{2}}{3}

To calculate d, we can use the fact that the distance between the center of mass of the combined body and the axis of rotation is equal to the distance between the center of mass of each lamina and the axis of rotation. This distance can be calculated using similar triangles (see diagram).

The distance between K and the axis of rotation can be written as:
d = \frac{a}{2}\left(\frac{1}{2}+\frac{1}{4}\right) = \