- #1
71GA
- 208
- 0
Lets say we have a finite square well symetric around ##y## axis (picture below).
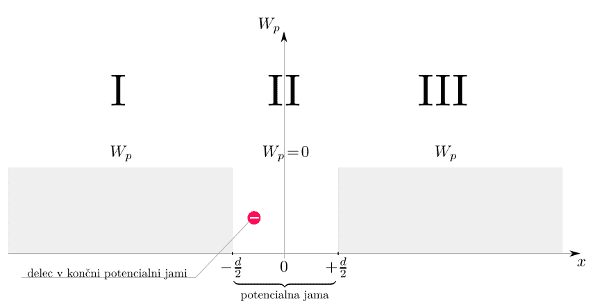
I know how and why general solutions to the second order ODE (stationary Schrödinger equation) are as follows for the regions I, II and III.
\begin{align}
\text{I:}& & \psi_{\text{I}}&= Ae^{\kappa x} \\
\text{III:}& & \psi_{\text{III}}&= Be^{-\kappa x} \\
\text{II:}& & \psi_{\text{II}}&= C \cos(k x) + D\sin(kx)
\end{align}
But now i got to a point where i have to start applying a boundary conditions to get a speciffic solution. So i start with the 1st boundary condition which is ##\psi_{\text{I}}\left(-\frac{d}{2}\right)=\psi_{\text{II}}\left(-\frac{d}{2}\right)## for the left potential shift and ##\psi_{\text{II}}\left(\frac{d}{2}\right)=\psi_{\text{III}}\left(\frac{d}{2}\right)## for the right potential shift. These leave me with a system of 2 equations (one for left and one for right potential shift):
\begin{align}
{\scriptsize\text{left potential shift:}}& & Ae^{-\kappa \frac{d}{2}} &= C \cos\left(k\tfrac{d}{2}\right) - D\sin\left(k \tfrac{d}{2}\right)\\
{\scriptsize \text{right potential shift:}}& & Be^{-\kappa \frac{d}{2}} &= C \cos\left(k\tfrac{d}{2}\right) + D\sin\left(k \tfrac{d}{2}\right)\\
\end{align}
Question 1:
From here on authors of most books don't seem to explain much. Most of them only say that we must use ##\boxed{D\!=\!0}## to solve for even solutions and ##\boxed{C\!=\!0}## to solve for *odd solutions*. What is this argument based on?
I know how and why general solutions to the second order ODE (stationary Schrödinger equation) are as follows for the regions I, II and III.
\begin{align}
\text{I:}& & \psi_{\text{I}}&= Ae^{\kappa x} \\
\text{III:}& & \psi_{\text{III}}&= Be^{-\kappa x} \\
\text{II:}& & \psi_{\text{II}}&= C \cos(k x) + D\sin(kx)
\end{align}
But now i got to a point where i have to start applying a boundary conditions to get a speciffic solution. So i start with the 1st boundary condition which is ##\psi_{\text{I}}\left(-\frac{d}{2}\right)=\psi_{\text{II}}\left(-\frac{d}{2}\right)## for the left potential shift and ##\psi_{\text{II}}\left(\frac{d}{2}\right)=\psi_{\text{III}}\left(\frac{d}{2}\right)## for the right potential shift. These leave me with a system of 2 equations (one for left and one for right potential shift):
\begin{align}
{\scriptsize\text{left potential shift:}}& & Ae^{-\kappa \frac{d}{2}} &= C \cos\left(k\tfrac{d}{2}\right) - D\sin\left(k \tfrac{d}{2}\right)\\
{\scriptsize \text{right potential shift:}}& & Be^{-\kappa \frac{d}{2}} &= C \cos\left(k\tfrac{d}{2}\right) + D\sin\left(k \tfrac{d}{2}\right)\\
\end{align}
Question 1:
From here on authors of most books don't seem to explain much. Most of them only say that we must use ##\boxed{D\!=\!0}## to solve for even solutions and ##\boxed{C\!=\!0}## to solve for *odd solutions*. What is this argument based on?
Last edited: