- #1
Rake-MC
- 325
- 0
The Problem
You are given: http://img530.imageshack.us/img530/4468/88346476ca9.jpg
Where http://img408.imageshack.us/img408/209/53113174nt5.jpg is constant (taken as B).
a) Differentiate both sides to produce a second order ODE for y(x)
b) Show that it can be written as a first order ODE for u=dy/dx
http://img229.imageshack.us/img229/5861/81200662fv5.jpg
c) Find the general solution for part b), you should have two arbitrary constants.
The fundamental theorem of calculus:
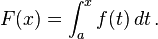
a) Using fundamental theorem of calculus, d2y/dx2 = Bf(x)
=> d2y/dx2 = B(1 + (dy/dx)2)1/2
b) Let u = dy/dx => du/dx = B(1 + (dy/dx)2)1/2 = B(1 + u2)1/2
c) Not a clue.. I have actually got no idea where to start for this. I would solve du/dx first, but wouldn't that just result in what I was given, the equation for part a)?
Thanks in advance.
You are given: http://img530.imageshack.us/img530/4468/88346476ca9.jpg
Where http://img408.imageshack.us/img408/209/53113174nt5.jpg is constant (taken as B).
a) Differentiate both sides to produce a second order ODE for y(x)
b) Show that it can be written as a first order ODE for u=dy/dx
http://img229.imageshack.us/img229/5861/81200662fv5.jpg
c) Find the general solution for part b), you should have two arbitrary constants.
Homework Equations
The fundamental theorem of calculus:
The Attempt at a Solution
a) Using fundamental theorem of calculus, d2y/dx2 = Bf(x)
=> d2y/dx2 = B(1 + (dy/dx)2)1/2
b) Let u = dy/dx => du/dx = B(1 + (dy/dx)2)1/2 = B(1 + u2)1/2
c) Not a clue.. I have actually got no idea where to start for this. I would solve du/dx first, but wouldn't that just result in what I was given, the equation for part a)?
Thanks in advance.
Last edited by a moderator: