- #1
mysearch
Gold Member
- 526
- 0
In another thread I was reminded that there is a `clear` distinction between `curved space` and `curved spacetime`. However, to be honest, I wasn’t sure that I really understood this difference and was pretty sure I couldn’t visualise it. So, by way of a learning process, I wanted to see if there was any way of providing a simplified, but possibly more intuitive visualisation of the nature of both `curved space` and `curved spacetime`. As such, the first 3 postings are simply some initial ideas and issues that I am trying to clarify.
Visualisations:
One of the first visualisation of curvature we often come across is the heavy ball on the rubber sheet. Of course, this image has its limitations in that it is just illustrating the curvature of 2D-space, i.e. time is not really being addressed, unless you assume one axis as time, but then observed time dilates on approach rather than expands.
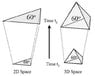
Next, we might consider the image of a sphere with a triangle on it, accompanied by a description that the angles of this triangle don’t add up to 180 degrees and the observation that 2 people walking due North from the Equator converge at the North Pole, i.e. parallel lines converging. Initially, this appears to be more relevant to spatial curvature, which in the context of the current cosmological model is said to be nearly flat, at least, within the current era.
The next image that is possibly more relevant to cosmology relates to the balloon analogy, which alludes to not only the curvature, but also the expansion of the universe. However, we are usually reminded that this visualisation only applies to the surface of the balloon, not its volume, which might leave the question as to what frame of reference is the surface of the balloon said to be curving around? Still, as often pointed out, it is only an analogy and should not be taken literally.
The following link seems to be a valid attempt to provide an initial visualisation of space and time curvature, which presumably combine to form a concept of spacetime curvature. http://www.math.gatech.edu/~berglund/GR.html
However, this presentation seems to be focused on the curvature resulting from the proximity to a large mass-density, which does not necessarily reflect the assumptions of a low mass density homogeneous universe that may or may not have a centre of gravity.
The next link is a much more sophisticated treatment, which includes a brief discussion of cosmological models from which I have extracted a diagram, attached below as Figure-6.jpg by way of quick reference. http://www.rpi.edu/dept/phys/Courses/Astronomy/CurvedSpacetimeAJP.pdf
However, I really wanted to see if I it was possible to provide a far simpler starting point for visualising the specific ideas of `flat space` and `curved spacetime` within a k=0 homogeneous expanding cosmological model. I fully accept that this attempt may end in failure . Even so, I will raise some specific issues for clarification in subsequent posts in order to keep each posting to a manageable length. Thanks
. Even so, I will raise some specific issues for clarification in subsequent posts in order to keep each posting to a manageable length. Thanks
--------------
Visualisations:
One of the first visualisation of curvature we often come across is the heavy ball on the rubber sheet. Of course, this image has its limitations in that it is just illustrating the curvature of 2D-space, i.e. time is not really being addressed, unless you assume one axis as time, but then observed time dilates on approach rather than expands.
Next, we might consider the image of a sphere with a triangle on it, accompanied by a description that the angles of this triangle don’t add up to 180 degrees and the observation that 2 people walking due North from the Equator converge at the North Pole, i.e. parallel lines converging. Initially, this appears to be more relevant to spatial curvature, which in the context of the current cosmological model is said to be nearly flat, at least, within the current era.
The next image that is possibly more relevant to cosmology relates to the balloon analogy, which alludes to not only the curvature, but also the expansion of the universe. However, we are usually reminded that this visualisation only applies to the surface of the balloon, not its volume, which might leave the question as to what frame of reference is the surface of the balloon said to be curving around? Still, as often pointed out, it is only an analogy and should not be taken literally.
The following link seems to be a valid attempt to provide an initial visualisation of space and time curvature, which presumably combine to form a concept of spacetime curvature. http://www.math.gatech.edu/~berglund/GR.html
However, this presentation seems to be focused on the curvature resulting from the proximity to a large mass-density, which does not necessarily reflect the assumptions of a low mass density homogeneous universe that may or may not have a centre of gravity.
The next link is a much more sophisticated treatment, which includes a brief discussion of cosmological models from which I have extracted a diagram, attached below as Figure-6.jpg by way of quick reference. http://www.rpi.edu/dept/phys/Courses/Astronomy/CurvedSpacetimeAJP.pdf
However, I really wanted to see if I it was possible to provide a far simpler starting point for visualising the specific ideas of `flat space` and `curved spacetime` within a k=0 homogeneous expanding cosmological model. I fully accept that this attempt may end in failure
 . Even so, I will raise some specific issues for clarification in subsequent posts in order to keep each posting to a manageable length. Thanks
. Even so, I will raise some specific issues for clarification in subsequent posts in order to keep each posting to a manageable length. ThanksAttachments
Last edited by a moderator: