- #1
sevag00
- 80
- 1
Homework Statement
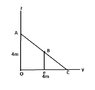
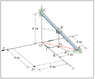
Determine the components of F that act along rod AC and perpendicular to it.
Given: B is located 3 m along the rod from end C.
The problem is that the coordinates of B aren't given so I'm having some trouble in finding the vector components of F along BD. If someone can give me a hint in finding the coordinates of B.