- #1
zaper
- 49
- 0
I've worked through this problem for a while now and can't quite come up with an answer. The problem is as follows:
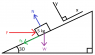
A block with mass 5 kg sits on an inclined plane of 30°. The coefficient of static friction is 0.1 between the plane and block. A force F is applied in the horizontal direction on the block. (I have attached a picture of the problem)
What is the minimum magnitude of F to keep the block from slipping?
What I have so far is this:
I assume then that since we're talking about static friction the block is not moving so there is no acceleration other than gravity anywhere.
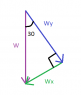
The weight of the block in the x direction (Wx) = mg*cos(30) and Wy = mg*sin(30)
The force of F in the x direction (Fx) = F*cos(30) and Fy = mg*sin(30)
The Normal force (N) = Wy + Fy
The maximum static friction (fs) = μ*N which I solved down to .1*(F+mg)*sin(30)
I then set Fx = fs to find the F for the maximum static friction and got F = 3.
However I believe that this is the maximum force such that the block will not move not the minimum.
Have I gone horribly awry here? What should I do next?
A block with mass 5 kg sits on an inclined plane of 30°. The coefficient of static friction is 0.1 between the plane and block. A force F is applied in the horizontal direction on the block. (I have attached a picture of the problem)
What is the minimum magnitude of F to keep the block from slipping?
What I have so far is this:
I assume then that since we're talking about static friction the block is not moving so there is no acceleration other than gravity anywhere.
The weight of the block in the x direction (Wx) = mg*cos(30) and Wy = mg*sin(30)
The force of F in the x direction (Fx) = F*cos(30) and Fy = mg*sin(30)
The Normal force (N) = Wy + Fy
The maximum static friction (fs) = μ*N which I solved down to .1*(F+mg)*sin(30)
I then set Fx = fs to find the F for the maximum static friction and got F = 3.
However I believe that this is the maximum force such that the block will not move not the minimum.
Have I gone horribly awry here? What should I do next?