- #1
gnittel
- 5
- 0
Hi guys! :)
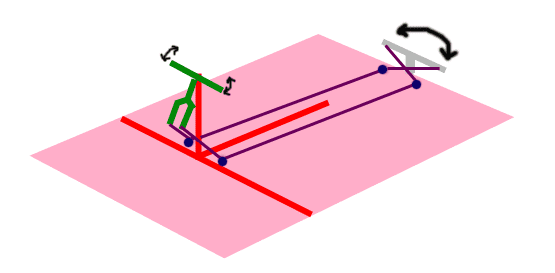
Ok so this image may look funny, but this is actually an attempt to design a bike that can propel on water. What you are seeing is bike's handlebar (green), mounted on a support (red). Its supposed to have a rudder system at the back (gray). The pink rectangle is the wood where everything is placed (the raft). You can also see violet lines, this represent the rope to be pulled by the handlebars so the rudder would move along.
Now, the problem is to determine the optimum placement of the 4 hooks on the wood (represented by the blue dots) that will enable the driver to have an easier steering. Hooks are 1 inch in height.
the end of the fork (where one end of the rope is tied) is 12 inches above the surface of the wood.
Restrictions:
the front of the supports must be cleared from anything, so the hooks are to be placed only somewhere near the blue dot.
Looking at one hook near the handle bars, I assigned a certain tension that is caused by the rudder (horizontal force) and a downward force by the hook. Problem is I don't think my process is correct. :(
Can someone tell me an good idea where to start? Thanks :)
Homework Statement
Ok so this image may look funny, but this is actually an attempt to design a bike that can propel on water. What you are seeing is bike's handlebar (green), mounted on a support (red). Its supposed to have a rudder system at the back (gray). The pink rectangle is the wood where everything is placed (the raft). You can also see violet lines, this represent the rope to be pulled by the handlebars so the rudder would move along.
Now, the problem is to determine the optimum placement of the 4 hooks on the wood (represented by the blue dots) that will enable the driver to have an easier steering. Hooks are 1 inch in height.
the end of the fork (where one end of the rope is tied) is 12 inches above the surface of the wood.
Restrictions:
the front of the supports must be cleared from anything, so the hooks are to be placed only somewhere near the blue dot.
The Attempt at a Solution
Looking at one hook near the handle bars, I assigned a certain tension that is caused by the rudder (horizontal force) and a downward force by the hook. Problem is I don't think my process is correct. :(
Can someone tell me an good idea where to start? Thanks :)