Force Required to pull a cylindrical cover

[vaas44]

1. Homework Statement

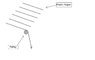
A plastic shade cover is almost 290 ft in length and 150 ft in breadth. It is wrapped around a cylindrical wooden rod which is at a height of 7 ft from the ground. The cover is pulled by nylon/plastic ropes to the right to its complete length of 290 ft. Consider the thickness of plastic cover to be 10 mm and density of plastic as 850 kg/m^3. The ropes are pulled by 7 people towards right. Diameter of the wooden rod is 10 cm and density 650 kg/m^3.

How much total force is required to pull the cover completely to the right?

Please give views on an efficient pulley system to reduce the effort by 1/3.

Homework Equations

3. I tried calculating angular acceleration of the cylindrical rod and to further determine the exact force required to pull the cover to its full length.

 

[jbsteele]

The Attempt at a Solution We can calculate the total force required to pull the cover to its full length by using the formula F = ma, where 'm' is the mass and 'a' is acceleration.Mass of the plastic shade cover = Volume x Density = (290 x 150 x 0.01) m^3 x 850 kg/m^3 = 4.26 x 10^4 kgMass of the wooden rod = Volume x Density = (π x (0.1/2)^2 x 7) m^3 x 650 kg/m^3 = 1.06 x 10^3 kgTotal mass = 4.26 x 10^4 + 1.06 x 10^3 = 4.37 x 10^4 kgAngular Acceleration = 2π(290/150)/7 = 2π(1.966666667) = 12.568075117 rad/s^2Total Force required to pull the cover completely to the right = Mass x Acceleration = 4.37 x 10^4 x 12.568075117 = 5.48 x 10^6 NThus, the total force required to pull the cover completely to the right is 5.48 x 10^6 N. To reduce the effort by 1/3, an efficient pulley system can be used. This pulley system will consist of two or more pulleys arranged in such a way that the force applied to pull the cover is reduced. This is possible because the load is shared by multiple pulleys, thus reducing the effort needed to pull the cover.